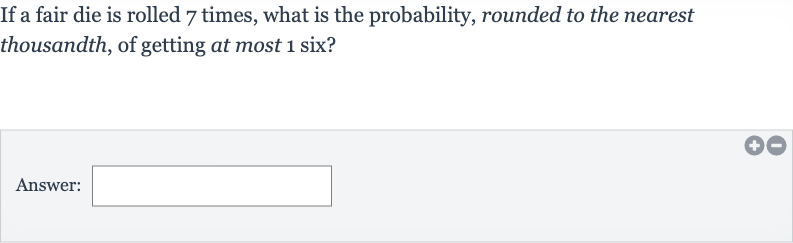
If a fair die is rolled 7 times, what is the probability, rounded to the nearest thousandth, of getting at most 1 six? Answer:

Question

Bytelearn · Accepted Answer

Understand the problem: Understand the problem. We need to calculate the probability of rolling at most one six in seven rolls of a fair die. This means we can have either zero sixes or one six in our rolls.Calculate single roll probability: Calculate the probability of rolling a six on a single roll. The probability of rolling a six on a single die is 1/6, and the probability of not rolling a six is 5/6.Calculate no sixes in seven rolls: Calculate the probability of rolling no sixes in seven rolls. The probability of not rolling a six in seven rolls is (5/6)^7.Calculate exactly one six: Calculate the probability of rolling exactly one six in seven rolls. The probability of rolling exactly one six can occur in any of the seven rolls. We can calculate this by multiplying the probability of rolling a six once (1/6) by the probability of not rolling a six in the other six rolls (5/6)^6, and then multiplying by the number of ways this can happen, which is 7 choose 1 (7C1).Calculate 7C1: Calculate 7C1. 7C1 is the number of combinations of rolling one six in seven rolls, which is 7.Calculate total probability: Calculate the total probability of rolling exactly one six. The total probability of rolling exactly one six is 7 * (1/6) * (5/6)^6.Add probabilities: Add the probabilities of rolling no sixes and exactly one six. The total probability of rolling at most one six is the sum of the probabilities of rolling no sixes and exactly one six: (5/6)^7 + 7 * (1/6) * (5/6)^6.Perform calculations: Perform the calculations. (5/6)^7 = 0.27908 (rounded to five decimal places) 7 * (1/6) * (5/6)^6 = 0.39013 (rounded to five decimal places) Adding these two probabilities gives us 0.27908 + 0.39013 = 0.66921.Round final probability: Round the final probability to the nearest thousandth. The final probability rounded to the nearest thousandth is 0.669.

If a fair die is rolled $7$ times, what is the probability, rounded to the nearest thousandth, of getting at most $1$ six? $\newline$ Answer:

Full solution

More problems from Find probabilities using the binomial distribution

Related topics

If a fair die is rolled 777 times, what is the probability, rounded to the nearest thousandth, of getting at most 111 six?\newlineAnswer:

If a fair die is rolled $7$ times, what is the probability, rounded to the nearest thousandth, of getting at most $1$ six? $\newline$ Answer: