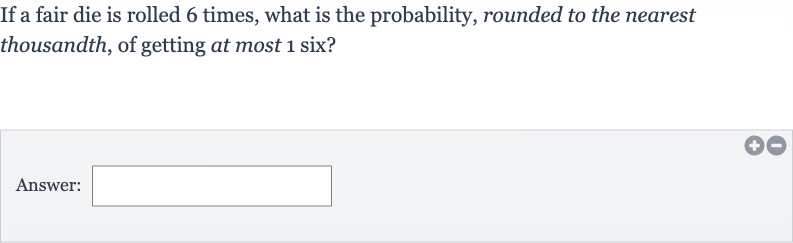
If a fair die is rolled $6$ times, what is the probability, rounded to the nearest thousandth, of getting at most $1$ six? $\newline$ Answer:

View step-by-step help

Home

Math Problems

Precalculus

Find probabilities using the binomial distribution

Full solution

Q. If a fair die is rolled

6

times, what is the probability, rounded to the nearest thousandth, of getting at most

1

six?

\newline

Answer:

Understand the problem: First, we need to understand the problem. We are looking for the probability of rolling at most one six in $6$ rolls of a fair six-sided die. This means we want the probability of rolling exactly zero sixes or exactly one six.
Calculate zero sixes probability: To calculate the probability of rolling exactly zero sixes, we use the formula for the probability of an event not happening, which is $(1 - \text{probability of the event happening})$ . The probability of rolling a six on a single roll is $\frac{1}{6}$ , so the probability of not rolling a six is $\frac{5}{6}$ .
Calculate one six probability: Now, since the die rolls are independent events, we can raise the probability of not rolling a six to the power of the number of rolls to find the probability of not rolling a six in all $6$ rolls. This is $(\frac{5}{6})^6$ .
Add probabilities: Calculating $(5/6)^6$ gives us the probability of rolling zero sixes in six rolls. $\newline$ $(5/6)^6 \approx 0.3349$
Round the result: Next, we calculate the probability of rolling exactly one six. This can happen in $6$ different ways since the six can appear in any one of the six rolls. The probability of rolling a six is $\frac{1}{6}$ , and the probability of not rolling a six in the other five rolls is $(\frac{5}{6})^5$ .
Round the result: Next, we calculate the probability of rolling exactly one six. This can happen in $6$ different ways since the six can appear in any one of the six rolls. The probability of rolling a six is $\frac{1}{6}$ , and the probability of not rolling a six in the other five rolls is $\left(\frac{5}{6}\right)^5$ .The probability of rolling exactly one six is $6 \times \left(\frac{1}{6}\right) \times \left(\frac{5}{6}\right)^5$ . $\newline$ $6 \times \left(\frac{1}{6}\right) \times \left(\frac{5}{6}\right)^5 \approx 0.4019$
Round the result: Next, we calculate the probability of rolling exactly one six. This can happen in $6$ different ways since the six can appear in any one of the six rolls. The probability of rolling a six is $\frac{1}{6}$ , and the probability of not rolling a six in the other five rolls is $\left(\frac{5}{6}\right)^5$ .The probability of rolling exactly one six is $6 \times \frac{1}{6} \times \left(\frac{5}{6}\right)^5$ . $\newline$ $6 \times \frac{1}{6} \times \left(\frac{5}{6}\right)^5 \approx 0.4019$ Now, we add the probabilities of rolling exactly zero sixes and exactly one six to find the total probability of rolling at most one six. $\newline$ $0.3349 + 0.4019 \approx 0.7368$
Round the result: Next, we calculate the probability of rolling exactly one six. This can happen in $6$ different ways since the six can appear in any one of the six rolls. The probability of rolling a six is $\frac{1}{6}$ , and the probability of not rolling a six in the other five rolls is $\left(\frac{5}{6}\right)^5$ .The probability of rolling exactly one six is $6 \times \frac{1}{6} \times \left(\frac{5}{6}\right)^5$ . $6 \times \frac{1}{6} \times \left(\frac{5}{6}\right)^5 \approx 0.4019$ Now, we add the probabilities of rolling exactly zero sixes and exactly one six to find the total probability of rolling at most one six. $0.3349 + 0.4019 \approx 0.7368$ Finally, we round the result to the nearest thousandth as requested. Rounded to the nearest thousandth, the probability is $0.737$ .