AI tutor
Full solution
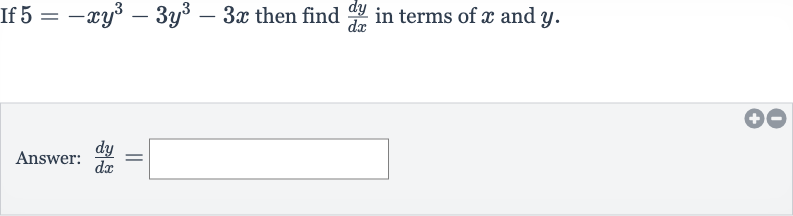
Q. If then find in terms of and .Answer:
- Given Equation: We are given the equation , and we need to find the derivative of with respect to , which is . To do this, we will use implicit differentiation, treating as a function of .
- Implicit Differentiation: Differentiate both sides of the equation with respect to . Remember that when differentiating terms with , we treat as a function of and use the chain rule to include .
- Product Rule: The derivative of a constant is , so . For , we use the product rule: , where and . So, . For , we simply multiply the derivative of by , which gives us . For , the derivative is simply .
- Combining Differentiated Terms: Now we combine all the differentiated terms:
- Isolating Terms: We need to solve for . First, we isolate the terms that contain on one side of the equation:.
- Factoring Out: Factor out from the left side of the equation:.
- Dividing Both Sides: Now, divide both sides by to solve for :.
- Simplifying the Denominator: We can simplify the denominator by factoring out :.