AI tutor
Full solution
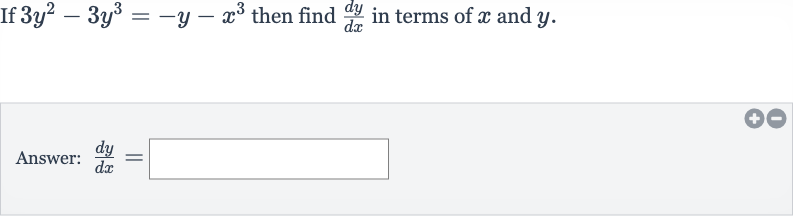
Q. If then find in terms of and .Answer:
- Differentiate both sides: First, we need to differentiate both sides of the equation with respect to . The left side of the equation is in terms of , which is a function of , so we will use the chain rule to differentiate it. The right side is already in terms of , so we can differentiate it directly.Differentiate the left side:Using the chain rule, we get:Differentiate the right side:Now we have the differentiated equation:
- Solve for : Next, we need to solve for . To do this, we will collect all the terms involving on one side of the equation and the remaining terms on the other side.Combine like terms:
- Isolate : Now, we isolate by dividing both sides of the equation by :This gives us the derivative of with respect to in terms of and .