AI tutor
Full solution
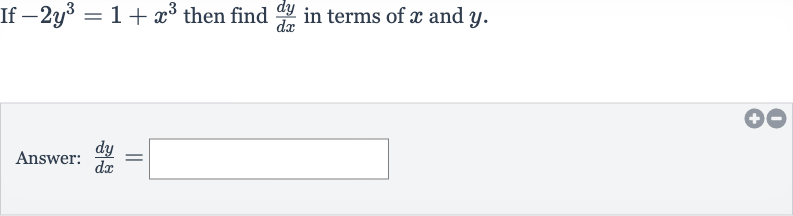
Q. If then find in terms of and .Answer:
- Write Equation: Write down the given equation.The given equation is .
- Differentiate with Respect: Differentiate both sides of the equation with respect to . To find , we need to differentiate both sides of the equation with respect to . Remember that is a function of , so when differentiating terms with , we use the chain rule.
- Apply Chain and Power Rule: Apply the chain rule to the left side and the power rule to the right side.Using the chain rule on the left side, we get . On the right side, the derivative of is , and the derivative of is .
- Solve for Solve for . To solve for , we divide both sides of the equation by .
- Simplify Expression: Simplify the expression for . We can simplify the fraction by dividing the numerator and the denominator by .