Full solution
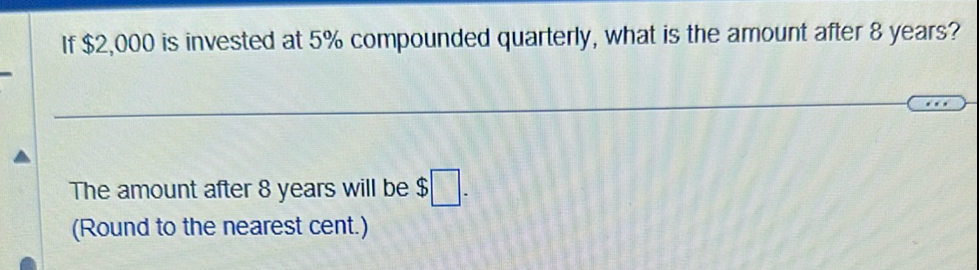
Q. If is invested at compounded quarterly, what is the amount after years?The amount after years will be .(Round to the nearest cent.)
- Identify Values: Identify the principal amount , the annual interest rate , the number of times the interest is compounded per year , and the number of years the money is invested . or (since interest is compounded quarterly) years
- Compound Interest Formula: Use the compound interest formula to calculate the final amount . The compound interest formula is . Substitute the values into the formula:
- Calculate Values: Calculate the values inside the parentheses and the exponent.Now the formula looks like this:
- Calculate Amount: Calculate the amount after years.Use a calculator to find :Now multiply this by the principal amount:
- Round Final Amount: Round the final amount to the nearest cent.
More problems from Exponential growth and decay: word problems
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help