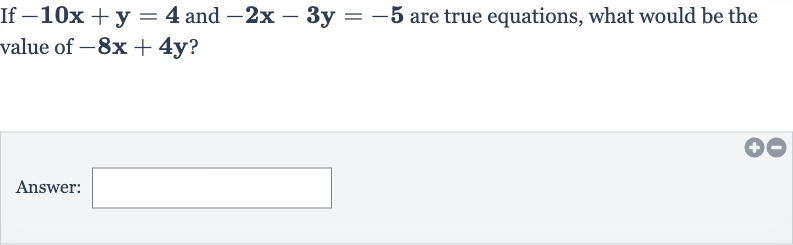If $-\mathbf{1 0 x}+\mathbf{y}=\mathbf{4}$ and $-\mathbf{2 x}-\mathbf{3 y}=-\mathbf{5}$ are true equations, what would be the value of $-8 x+4 y$ ? $\newline$ Answer:

View step-by-step help

Home

Math Problems

Grade 8

Describe the graph of a linear equation

Full solution

Q. If

-\mathbf{1 0 x}+\mathbf{y}=\mathbf{4}

and

-\mathbf{2 x}-\mathbf{3 y}=-\mathbf{5}

are true equations, what would be the value of

-8 x+4 y

\newline

Answer:

Identify Equations: Identify the system of equations to solve for $x$ and $y$ . We have the following system of equations: $1$ ) $-10x + y = 4$ $2$ ) $-2x - 3y = -5$
Isolate y: Isolate $y$ in the first equation to use it for substitution. $\newline$ From equation $1)$ , we get: $\newline$ $y = 10x + 4$
Substitute and Solve: Substitute the expression for $y$ from equation $1$ ) into equation $2$ ). $\newline$ Plugging $y = 10x + 4$ into equation $2$ ), we get: $\newline$ $-2x - 3(10x + 4) = -5$
Combine Terms: Distribute and combine like terms in the substituted equation. $\newline$ $-2x - 30x - 12 = -5$ $\newline$ $-32x - 12 = -5$
Isolate x: Add $12$ to both sides of the equation to isolate the term with $x$ . $\newline$ $-32x - 12 + 12 = -5 + 12$ $\newline$ $-32x = 7$
Solve for x: Divide both sides by $-32$ to solve for x. $\newline$ $x = \frac{7}{-32}$ $\newline$ $x = -\frac{7}{32}$
Substitute for y: Substitute the value of $x$ back into the expression for $y$ . $y = 10\left(-\frac{7}{32}\right) + 4$ $y = -\frac{70}{32} + 4$
Combine Fractions: Convert $4$ to a fraction with a denominator of $32$ to combine with $-\frac{70}{32}$ . $\newline$ $4 = \frac{128}{32}$ $\newline$ $y = -\frac{70}{32} + \frac{128}{32}$
Add Fractions: Add the fractions to find the value of $y$ . $y = (-70 + 128) / 32$ $y = 58/32$ $y = 29/16$
Calculate Expression: Now that we have the values of $x$ and $y$ , calculate $-8x + 4y$ . $\newline$ $-8x + 4y = -8(-\frac{7}{32}) + 4(\frac{29}{16})$
Simplify Expression: Multiply the values to simplify the expression. $\newline$ $-8x + 4y = \frac{56}{32} + \frac{116}{16}$
Convert to Decimal: Simplify the fractions by reducing them to the same denominator or converting to whole numbers. $\newline$ $\frac{56}{32} = \frac{7}{4}$ (since $56$ and $32$ are both divisible by $8$ ) $\newline$ $\frac{116}{16} = 7.25$ (since $116$ divided by $16$ is $7.25$ ) $\newline$ $-8x + 4y = \frac{7}{4} + 7.25$
Add Values: Convert $\frac{7}{4}$ to a decimal to add it to $7.25$ . $\newline$ $\frac{7}{4} = 1.75$ $\newline$ $-8x + 4y = 1.75 + 7.25$
Add Values: Convert $\frac{7}{4}$ to a decimal to add it to $7.25$ . $\newline$ $\frac{7}{4} = 1.75$ $\newline$ $-8x + 4y = 1.75 + 7.25$ Add the decimal values to find the final answer. $\newline$ $-8x + 4y = 1.75 + 7.25$ $\newline$ $-8x + 4y = 9$