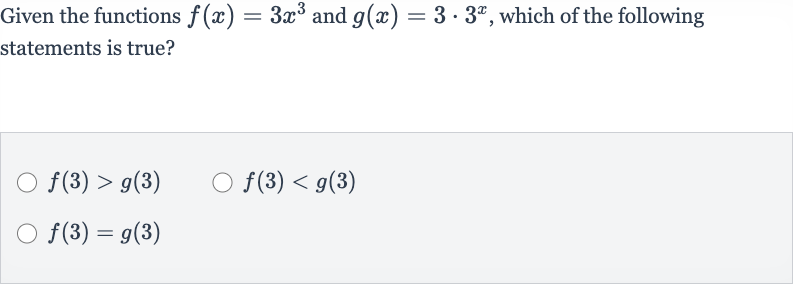Full solution
Q. Given the functions and , which of the following statements is true?
- Calculate : Calculate using the function .
- Calculate : Calculate using the function .
- Compare values: Compare the values of and .Since and , we have .
More problems from Solve quadratic inequalities
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help