AI tutor
Full solution
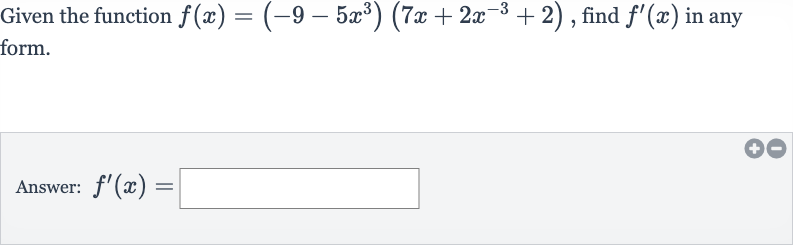
Q. Given the function , find in any form.Answer:
- Apply Product Rule: First, we need to apply the product rule to find the derivative of the function . The product rule states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function.
- Define Functions: Let's denote the two functions as and . We need to find the derivatives and .
- Find Derivatives: The derivative of with respect to is .
- Apply Product Rule: The derivative of with respect to is .
- Substitute Expressions: Now we apply the product rule: .
- Simplify Expression: Substitute the expressions for , , , and into the product rule formula: .
- Combine Like Terms: Simplify the expression by multiplying the terms: .
- Combine Like Terms: Simplify the expression by multiplying the terms: .Combine like terms to get the final derivative in any form: .
More problems from Composition of linear and quadratic functions: find an equation
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help