Full solution
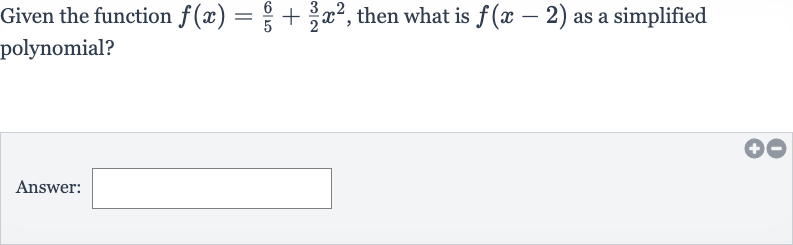
Q. Given the function , then what is as a simplified polynomial?Answer:
- Understand Function: Understand the function and what is being asked.We are given the function and we need to find . This means we need to substitute for in the function .
- Substitute : Substitute for in the function .
- Expand Squared Term: Expand the squared term .
- Substitute Expanded Term: Substitute the expanded term back into the function.
- Distribute Constant: Distribute the across the terms in the parentheses.
- Simplify Expression: Simplify the expression by multiplying the constants.
- Combine Constant Terms: Combine the constant terms and .
To combine and , we need to express as a fraction with a denominator of . - Add Constant Fractions: Add the constant fractions.
- Write Final Polynomial: Write the final simplified polynomial.
More problems from Composition of linear and quadratic functions: find an equation
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help