Full solution
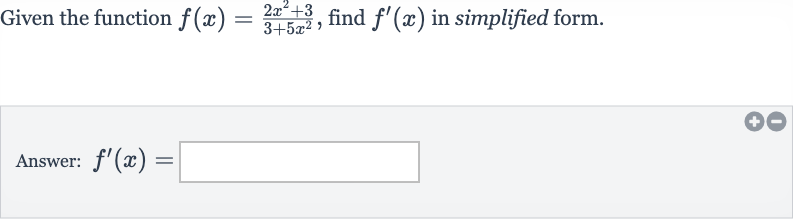
Q. Given the function , find in simplified form.Answer:
- Apply Quotient Rule: To find the derivative of the function , we will use the quotient rule. The quotient rule states that if we have a function , then . Here, and .
- Find : First, we need to find the derivative of . The derivative of is , and the derivative of is , so .
- Find : Next, we need to find the derivative of . The derivative of is , and the derivative of is , so .
- Plug into Quotient Rule: Now we apply the quotient rule. We have and , so we plug these into the quotient rule formula:
- Simplify Numerator: We simplify the numerator of the derivative:
- Factor Out : We can simplify the derivative further by factoring out a from the numerator:
More problems from Composition of linear and quadratic functions: find an equation
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help