Full solution
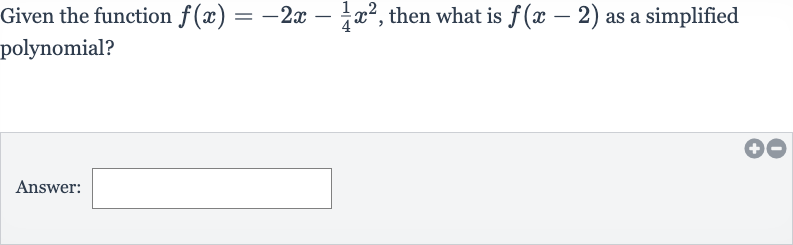
Q. Given the function , then what is as a simplified polynomial?Answer:
- Substitute and Distribute: To find , we need to substitute for every instance of in the function .
- Expand : First, distribute the across the term.
- Substitute Expanded Term: Next, expand the term.
- Distribute : Now, substitute the expanded back into the equation.
- Combine Like Terms: Distribute the across the .
- Reorder to Standard Form: Combine like terms.
- Reorder to Standard Form: Combine like terms.Reorder the terms to write the polynomial in standard form, which is from highest degree to lowest degree.
More problems from Composition of linear and quadratic functions: find an equation
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help