Full solution
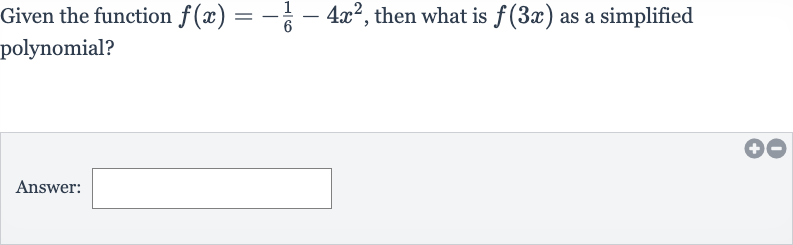
Q. Given the function , then what is as a simplified polynomial?Answer:
- Understand Function: Understand the function and what is being asked.We are given the function and we need to find , which means we need to substitute for every in the function .
- Substitute : Substitute into the function.Now we need to simplify the expression.
- Simplify Squared Term: Simplify the squared term.Now we substitute this back into the expression.
- Multiply Constants: Multiply the constants with the squared term.Now we substitute this back into the expression.
- Combine Terms: Combine the terms to get the final simplified polynomial. This is the simplified polynomial for .
More problems from Composition of linear and quadratic functions: find an equation
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help