Full solution
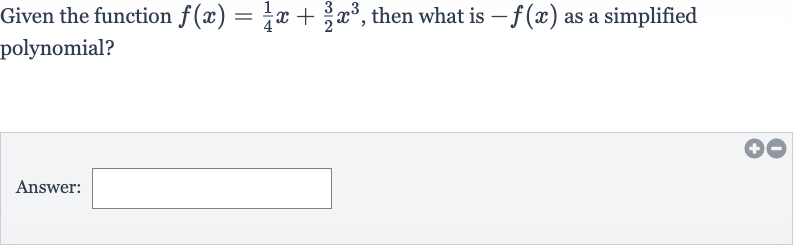
Q. Given the function , then what is as a simplified polynomial?Answer:
- Multiply by : To find , we need to multiply each term in the function by .
Now, multiply each term by :
-f(x) = -(\frac{\(1\)}{\(4\)})x - (\frac{\(3\)}{\(2\)})x^\(3 - Check for Errors: Check for any math errors in the previous step. We correctly multiplied each term by , so there are no math errors.
- Simplify if Necessary: Simplify the expression if necessary. However, the expression is already in its simplest form, so no further simplification is needed.
More problems from Composition of linear and quadratic functions: find an equation
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help