Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Given the function f(x)=(-1-10 x+5x^(-2))(6x^(-2)-9), find f^(')(x) in any form. Answer: f^(')(x)=

Given the function f(x)=(−1−10x+5x−2)(6x−2−9) f(x)=\left(-1-10 x+5 x^{-2}\right)\left(6 x^{-2}-9\right) , find f′(x) f^{\prime}(x) in any form.\newlineAnswer: f′(x)= f^{\prime}(x)=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Composition of linear and quadratic functions: find an equationright chevron icon

Full solution

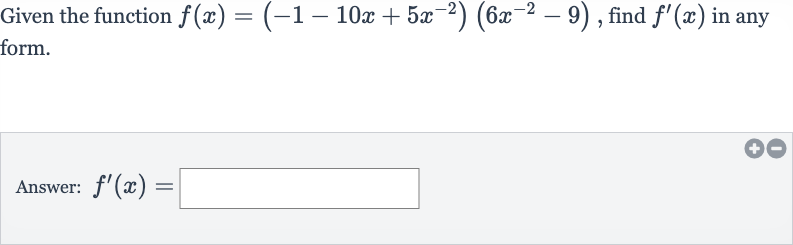
Q. Given the function f(x)=(−1−10x+5x−2)(6x−2−9) f(x)=\left(-1-10 x+5 x^{-2}\right)\left(6 x^{-2}-9\right) , find f′(x) f^{\prime}(x) in any form.\newlineAnswer: f′(x)= f^{\prime}(x)=
  1. Product Rule Explanation: To find the derivative of the function f(x)f(x), we will use the product rule, which states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function. The product rule is given by (u⋅v)′=u′⋅v+u⋅v′(u \cdot v)' = u' \cdot v + u \cdot v', where uu and vv are functions of xx.
  2. Identifying Functions: First, let's identify the two functions that are being multiplied:\newlineu(x)=−1−10x+5x−2u(x) = -1 - 10x + 5x^{-2}\newlinev(x)=6x−2−9v(x) = 6x^{-2} - 9\newlineNow we will find the derivatives of u(x)u(x) and v(x)v(x) separately.
  3. Derivative of u(x)u(x): The derivative of u(x)u(x) with respect to xx is:\newlineu′(x)=ddx(−1)−ddx(10x)+ddx(5x−2)u'(x) = \frac{d}{dx}(-1) - \frac{d}{dx}(10x) + \frac{d}{dx}(5x^{-2})\newlineu′(x)=0−10+ddx(5⋅x−2)u'(x) = 0 - 10 + \frac{d}{dx}(5 \cdot x^{-2})\newlineu′(x)=−10−10⋅x−3u'(x) = -10 - 10 \cdot x^{-3}
  4. Derivative of v(x)v(x): The derivative of v(x)v(x) with respect to xx is: v′(x)=ddx(6x−2)−ddx(9)v'(x) = \frac{d}{dx}(6x^{-2}) - \frac{d}{dx}(9) v′(x)=−12⋅x−3−0v'(x) = -12 \cdot x^{-3} - 0 v′(x)=−12⋅x−3v'(x) = -12 \cdot x^{-3}
  5. Applying Product Rule: Now, we apply the product rule to find f′(x)f'(x):f′(x)=u′(x)⋅v(x)+u(x)⋅v′(x)f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x)f′(x)=(−10−10⋅x−3)⋅(6x−2−9)+(−1−10x+5x−2)⋅(−12⋅x−3)f'(x) = (-10 - 10 \cdot x^{-3}) \cdot (6x^{-2} - 9) + (-1 - 10x + 5x^{-2}) \cdot (-12 \cdot x^{-3})
  6. Simplifying Expression: We simplify the expression by multiplying the terms: f′(x)=(−10×6x−2+10×9)+(10×6x−5−10×9x−3)+(12x−3+120x−2−60x−5)f'(x) = (-10 \times 6x^{-2} + 10 \times 9) + (10 \times 6x^{-5} - 10 \times 9x^{-3}) + (12x^{-3} + 120x^{-2} - 60x^{-5})
  7. Combine Like Terms: Combine like terms and simplify the expression:\newlinef′(x)=(−60x−2+90)+(60x−5−90x−3)+(12x−3+120x−2−60x−5)f'(x) = (-60x^{-2} + 90) + (60x^{-5} - 90x^{-3}) + (12x^{-3} + 120x^{-2} - 60x^{-5})\newlinef′(x)=−60x−2+90+60x−5−90x−3+12x−3+120x−2−60x−5f'(x) = -60x^{-2} + 90 + 60x^{-5} - 90x^{-3} + 12x^{-3} + 120x^{-2} - 60x^{-5}\newlinef′(x)=60x−2+2x−3−60x−5f'(x) = 60x^{-2} + 2x^{-3} - 60x^{-5}
  8. Final Derivative: Finally, we write the derivative in a more conventional form by using positive exponents:\newlinef′(x)=60x2+2x3−60x5f'(x) = \frac{60}{x^2} + \frac{2}{x^3} - \frac{60}{x^5}

More problems from Composition of linear and quadratic functions: find an equation

Question
Find the inverse of the function. y=x+3 y = x + 3 Write your answer in the form ax+b ax + b . Simplify any fractions. y= y = _____
Get tutor helpright-arrow

Posted 5 months ago

Question
Find (r∘s)(x)(r \circ s)(x).\newliner(x) = 33x\newlines(x) = 22x + 55\newlineWrite your answer as a polynomial in simplest form.\newline(r∘s)(x)=(r \circ s)(x) = ____
Get tutor helpright-arrow

Posted 7 months ago

Question
What is (f+g)(x)(f + g)(x)?\newlinef(x)=−3xf(x) = -3x\newlineg(x)=3x+1g(x) = 3x + 1\newline\newlineWrite your answer as a polynomial or a rational function in simplest form.\newline‾\underline{\hspace{3cm}}\newline
Get tutor helpright-arrow

Posted 7 months ago

Question
What is (f∗g)(x)(f * g)(x)?\newlinef(x)=−x+4f(x) = -x + 4\newlineg(x)=4xg(x) = 4x\newline\newlineWrite your answer as a polynomial or a rational function in simplest form.\newline‾\underline{\hspace{3em}}\newline
Get tutor helpright-arrow

Posted 7 months ago

Question
What is the domain of (fg)(x)\left(\frac{f}{g}\right)(x)?\newlinef(x)=2xf(x) = 2x\newlineg(x)=−5x+3g(x) = -5x + 3\newlineChoices:\newline[A]All real numbers[\text{A]All real numbers}\newline[B]All real numbers except 35[\text{B]All real numbers except } \frac{3}{5}\newline[C]All real numbers except −35[\text{C]All real numbers except } -\frac{3}{5}\newline[D]All real numbers except 53[\text{D]All real numbers except } \frac{5}{3}
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the inverse of the function.\newliney = −3x-3x \newlineWrite your answer in the form ax+bax + b. Simplify any fractions.\newliney = ______
Get tutor helpright-arrow

Posted 7 months ago

Question
Find (f∘g)(0)(f \circ g)(0).\newlinef(x)=6xf(x) = 6x\newlineg(x)=x2+4xg(x) = x^2 + 4x\newline(f∘g)(0)=(f \circ g)(0) = ____
Get tutor helpright-arrow

Posted 7 months ago

Question
Find (f∘g)(x)(f \circ g)(x).\newlinef(x)=x2+5f(x) = x^2 + 5\newlineg(x)=4xg(x) = 4x\newlineWrite your answer as a polynomial in simplest form.\newline(f∘g)(x)=(f \circ g)(x) = ______
Get tutor helpright-arrow

Posted 7 months ago

Question
Is f(x) f(x) the inverse function of g(x) g(x) ?\newlinef(x)=x f(x) = x \newlineg(x)=−4x g(x) = -4x \newlineChoices:\newline[yes] \text{[yes]} \newline[no] \text{[no]}
Get tutor helpright-arrow

Posted 7 months ago

Question
What is (f∗g)(x)(f * g)(x)? f(x)=3x2+9xf(x) = 3x^2 + 9x g(x)=3xg(x) = 3x Write your answer as a polynomial or a rational function in simplest form. ______
Get tutor helpright-arrow

Posted 5 months ago

View all (99)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant