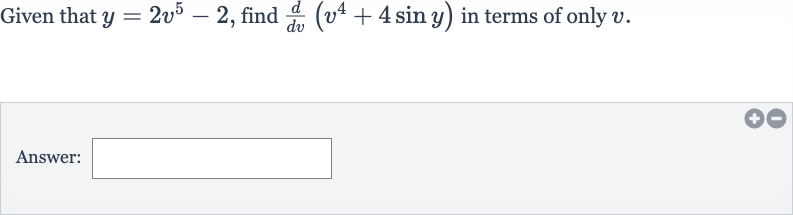
Given that y=2v^(5)-2, find (d)/(dv)(v^(4)+4sin y) in terms of only v. Answer:

Question

Given that  y=2v^(5)-2, find  (d)/(dv)(v^(4)+4sin y) in terms of only  v. Answer:

Bytelearn · Accepted Answer

Find Derivative with Chain Rule: We need to find the derivative of the expression (v^(4) + 4sin y) with respect to v. To do this, we will use the chain rule, which states that the derivative of a composite function is the derivative of the outer function times the derivative of the inner function. In this case, the outer function is v^(4) + 4sin(y), and the inner function is y, which is a function of v.Derivative of Outer Function: First, let's find the derivative of the outer function with respect to y. The derivative of v^(4) with respect to y is 0, since v^(4) does not depend on y. The derivative of 4sin(y) with respect to y is 4cos(y). So, the derivative of the outer function with respect to y is 4cos(y).Derivative of Inner Function: Next, we need to find the derivative of the inner function y with respect to v. We are given that y = 2v^(5) - 2. The derivative of y with respect to v is dy/dv = 10v^(4).Apply Chain Rule: Now, we apply the chain rule. The derivative of (v^(4) + 4sin y) with respect to v is the derivative of the outer function with respect to y times the derivative of y with respect to v. This gives us (0 + 4cos(y)) * (10v^(4)).Simplify Expression: Simplify the expression to get the derivative in terms of v. We have 4cos(y) * 10v^(4) = 40v^(4)cos(y).Express Cosine in Terms of v: We need to express cos(y) in terms of v. Since y = 2v^(5) - 2, we cannot directly substitute y into the cosine function. However, we can note that without the specific value of y, we cannot express cos(y) purely in terms of v. Therefore, the final derivative in terms of v and y is 40v^(4)cos(y).

Given that $y=2 v^{5}-2$ , find $\frac{d}{d v}\left(v^{4}+4 \sin y\right)$ in terms of only $v$ . $\newline$ Answer:

Full solution

More problems from Find the roots of factored polynomials

Related topics

Given that y=2v5−2 y=2 v^{5}-2 y=2v5−2, find ddv(v4+4sin⁡y) \frac{d}{d v}\left(v^{4}+4 \sin y\right) dvd​(v4+4siny) in terms of only v v v.\newlineAnswer:

Given that $y=2 v^{5}-2$ , find $\frac{d}{d v}\left(v^{4}+4 \sin y\right)$ in terms of only $v$ . $\newline$ Answer: