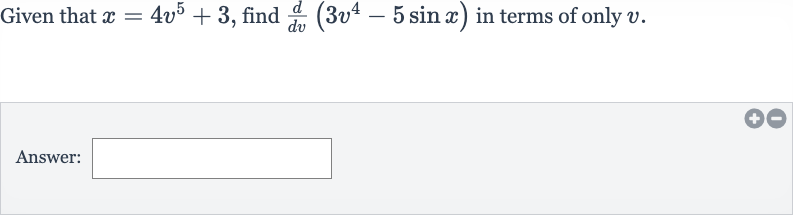
Given that x=4v^(5)+3, find (d)/(dv)(3v^(4)-5sin x) in terms of only v. Answer:

Question

Given that  x=4v^(5)+3, find  (d)/(dv)(3v^(4)-5sin x) in terms of only  v. Answer:

Bytelearn · Accepted Answer

Find Derivative of 3v^4: First, we need to find the derivative of the function 3v^4 with respect to v. The derivative of v^n with respect to v is n*v^(n-1). So, the derivative of 3v^4 with respect to v is 4*3v^(4-1) = 12v^3.Chain Rule for -5sin(x): Next, we need to find the derivative of -5sin(x) with respect to v. Since x is a function of v, we will use the chain rule. The chain rule states that the derivative of f(g(v)) with respect to v is f'(g(v))*g'(v). Here, f(x) = -5sin(x) and g(v) = 4v^5 + 3.Derivative of -5sin(x): We first find the derivative of f(x) = -5sin(x) with respect to x, which is -5cos(x).Derivative of 4v^5 + 3: Now we find the derivative of g(v) = 4v^5 + 3 with respect to v, which is 20v^4.Apply Chain Rule: Applying the chain rule, we multiply the derivative of f with respect to x by the derivative of g with respect to v. This gives us the derivative of -5sin(x) with respect to v as -5cos(x) * 20v^4.Express cos(x) in terms of v: Now we need to express cos(x) in terms of v, since x = 4v^5 + 3. However, there is no straightforward algebraic way to express cos(4v^5 + 3) in terms of v, so we leave it as cos(4v^5 + 3).Combine Derivatives: Combining the derivatives of 3v^4 and -5sin(x) with respect to v, we get the total derivative as 12v^3 - 5cos(4v^5 + 3) * 20v^4.Simplify Final Answer: Simplify the expression to get the final answer. 12v^3 - 100v^4cos(4v^5 + 3) is the derivative of 3v^4 - 5sin(x) with respect to v in terms of v.

Given that $x=4 v^{5}+3$ , find $\frac{d}{d v}\left(3 v^{4}-5 \sin x\right)$ in terms of only $v$ . $\newline$ Answer:

Full solution

More problems from Find the roots of factored polynomials

Related topics

Given that x=4v5+3 x=4 v^{5}+3 x=4v5+3, find ddv(3v4−5sin⁡x) \frac{d}{d v}\left(3 v^{4}-5 \sin x\right) dvd​(3v4−5sinx) in terms of only v v v.\newlineAnswer:

Given that $x=4 v^{5}+3$ , find $\frac{d}{d v}\left(3 v^{4}-5 \sin x\right)$ in terms of only $v$ . $\newline$ Answer: