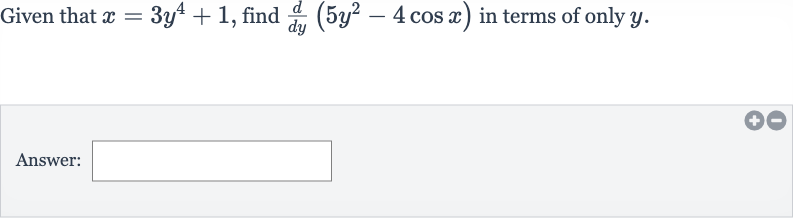
Given that x=3y^(4)+1, find (d)/(dy)(5y^(2)-4cos x) in terms of only y. Answer:

Question

Given that  x=3y^(4)+1, find  (d)/(dy)(5y^(2)-4cos x) in terms of only  y. Answer:

Bytelearn · Accepted Answer

Apply Chain Rule: To find the derivative of the function 5y^2 - 4cos(x) with respect to y, we need to apply the chain rule because x is a function of y. The chain rule states that the derivative of a composite function is the derivative of the outer function times the derivative of the inner function.Find Outer Function Derivative: First, let's find the derivative of the outer function 5y^2 - 4cos(x) with respect to x, which we will denote as f'(x). The derivative of 5y^2 with respect to x is 0 since y is treated as a constant with respect to x. The derivative of -4cos(x) with respect to x is 4sin(x). So, f'(x) = 0 + 4sin(x).Find Inner Function Derivative: Now, we need to find the derivative of the inner function x with respect to y, which we will denote as dx/dy. Given that x = 3y^4 + 1, the derivative of x with respect to y is dx/dy = d/dy(3y^4 + 1) = 12y^3.Apply Chain Rule Again: Using the chain rule, the derivative of the function 5y^2 - 4cos(x) with respect to y is the product of f'(x) and dx/dy. Therefore, (d/dy)(5y^2 - 4cos(x)) = f'(x) * dx/dy = 4sin(x) * 12y^3.Express Derivative in Terms of y: We need to express the derivative in terms of y only. Since x = 3y^4 + 1, we can substitute this into the sine function. So, sin(x) becomes sin(3y^4 + 1).Write Final Expression: Now, we can write the final expression for the derivative in terms of y: (d/dy)(5y^2 - 4cos(x)) = 4sin(3y^4 + 1) * 12y^3 = 48y^3sin(3y^4 + 1).

Given that $x=3 y^{4}+1$ , find $\frac{d}{d y}\left(5 y^{2}-4 \cos x\right)$ in terms of only $y$ . $\newline$ Answer:

Full solution

More problems from Find the roots of factored polynomials

Related topics

Given that x=3y4+1 x=3 y^{4}+1 x=3y4+1, find ddy(5y2−4cos⁡x) \frac{d}{d y}\left(5 y^{2}-4 \cos x\right) dyd​(5y2−4cosx) in terms of only y y y.\newlineAnswer:

Given that $x=3 y^{4}+1$ , find $\frac{d}{d y}\left(5 y^{2}-4 \cos x\right)$ in terms of only $y$ . $\newline$ Answer: