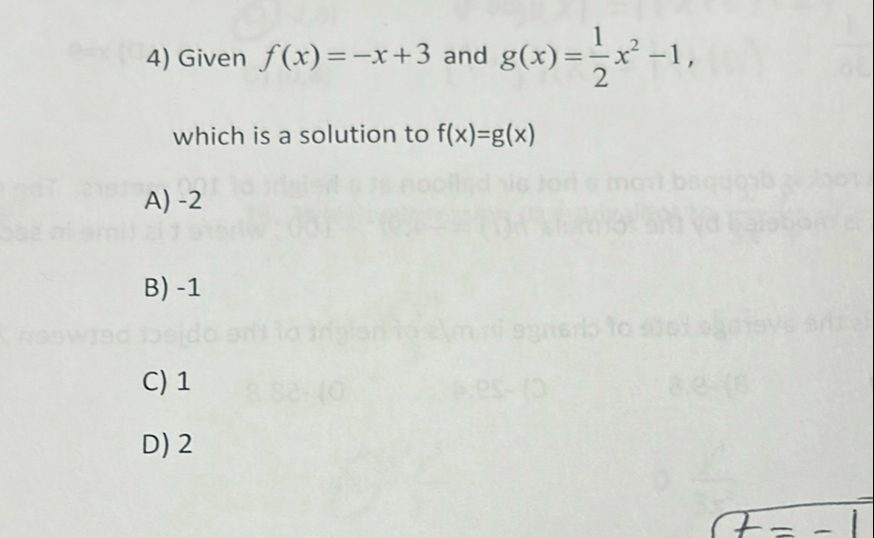Given f(x)=-x+3 and g(x)=(1)/(2)x^(2)-1, which is a solution to f(x)=g(x) A) -2 B) -1 C) 1 D) 2

Question

Given  f(x)=-x+3 and  g(x)=(1)/(2)x^(2)-1, which is a solution to  f(x)=g(x) A) -2 B) -1 C) 1 D) 2

Bytelearn · Accepted Answer

Set Equation Equal: To find the solution to f(x) = g(x), we need to set the two functions equal to each other and solve for x. So, we have the equation -x + 3 = (1/2)x^2 - 1.Form Quadratic Equation: First, let's move all terms to one side of the equation to set it to zero and form a quadratic equation. We add x and subtract 3 from both sides to get: (1/2)x^2 + x - 4 = 0.Eliminate Fraction: To make the equation easier to solve, we can multiply every term by 2 to get rid of the fraction: 2 * (1/2)x^2 + 2 * x - 2 * 4 = 0 * 2, which simplifies to: x^2 + 2x - 8 = 0.Factor Quadratic Equation: Now, we need to factor the quadratic equation, if possible. The factors of -8 that add up to 2 are 4 and -2. So, we can write the equation as: (x + 4)(x - 2) = 0.Apply Zero Product Property: Next, we apply the zero product property, which states that if a product of two factors is zero, then at least one of the factors must be zero. So, we set each factor equal to zero: x + 4 = 0 or x - 2 = 0.Solve for x: Solving each equation for x gives us the possible solutions: x = -4 or x = 2.Check Answer Choices: We need to check which of these solutions is given in the answer choices. The choices are A) -2, B) -1, C) 1, D) 2. Only x = 2 is in the answer choices, so x = -4 is not a valid option for this problem.Verify Solution: Finally, we can verify that x = 2 is indeed a solution by substituting it back into the original equations f(x) and g(x) to see if they are equal. For f(x), we have f(2) = -2 + 3 = 1. For g(x), we have g(2) = (1/2)(2)^2 - 1 = (1/2)(4) - 1 = 2 - 1 = 1. Since f(2) = g(2), x = 2 is a solution to f(x) = g(x).

Given $f(x)=-x+3$ and $g(x)=\frac{1}{2} x^{2}-1$ , which is a solution to $f(x)=g(x)$ $\newline$ A) $-2$ $\newline$ B) $-1$ $\newline$ C) $1$ $\newline$ D) $2$

Full solution

More problems from Transformations of functions

Related topics

Given f(x)=−x+3 f(x)=-x+3 f(x)=−x+3 and g(x)=12x2−1 g(x)=\frac{1}{2} x^{2}-1 g(x)=21​x2−1, which is a solution to f(x)=g(x) f(x)=g(x) f(x)=g(x)\newlineA) −2-2−2\newlineB) −1-1−1\newlineC) 111\newlineD) 222

Given $f(x)=-x+3$ and $g(x)=\frac{1}{2} x^{2}-1$ , which is a solution to $f(x)=g(x)$ $\newline$ A) $-2$ $\newline$ B) $-1$ $\newline$ C) $1$ $\newline$ D) $2$