Use the rational zeros theorem to determine the potential rational zeros of the polynomial function. Do not find the zeros. $\newline$ $f(x)=x^{3}-6 x-81$ $\newline$ List the possible potential rational zeros of the polynomial function. $\newline$ $\square$

Full solution

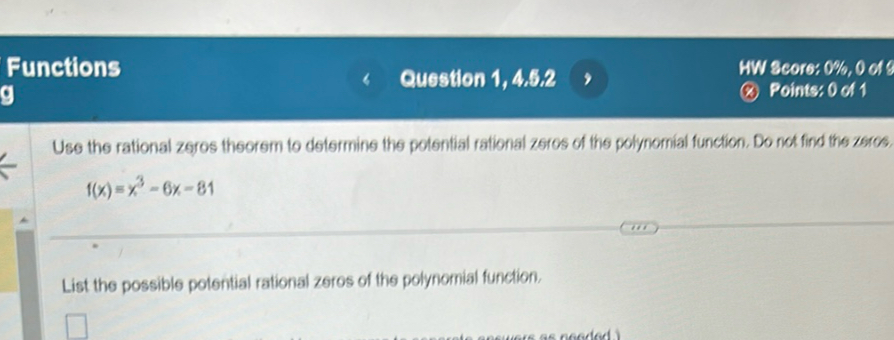
Q. Use the rational zeros theorem to determine the potential rational zeros of the polynomial function. Do not find the zeros.

\newline

f(x)=x^{3}-6 x-81

\newline

List the possible potential rational zeros of the polynomial function.

\newline

\square

Identify Terms: Identify the constant term and the leading coefficient of the polynomial. The constant term in the polynomial $f(x) = x^3 - 6x - 81$ is $-81$ , and the leading coefficient (the coefficient of the highest power of $x$ ) is $1$ .
List Factors: List the factors of the constant term and the leading coefficient. $\newline$ The factors of the constant term $-81$ are $\pm1$ , $\pm3$ , $\pm9$ , $\pm27$ , $\pm81$ . $\newline$ The factors of the leading coefficient $1$ are $\pm1$ .
Apply Theorem: Apply the Rational Zeros Theorem. $\newline$ The Rational Zeros Theorem states that any rational zero of the polynomial function $f(x)$ can be expressed in the form $\frac{p}{q}$ , where $p$ is a factor of the constant term and $q$ is a factor of the leading coefficient.
List Potential Zeros: List the potential rational zeros. $\newline$ The potential rational zeros are all the possible fractions formed by dividing the factors of the constant term by the factors of the leading coefficient. Since the leading coefficient is $1$ , the potential rational zeros are simply the factors of the constant term. $\newline$ The potential rational zeros are $\pm 1$ , $\pm 3$ , $\pm 9$ , $\pm 27$ , $\pm 81$ .