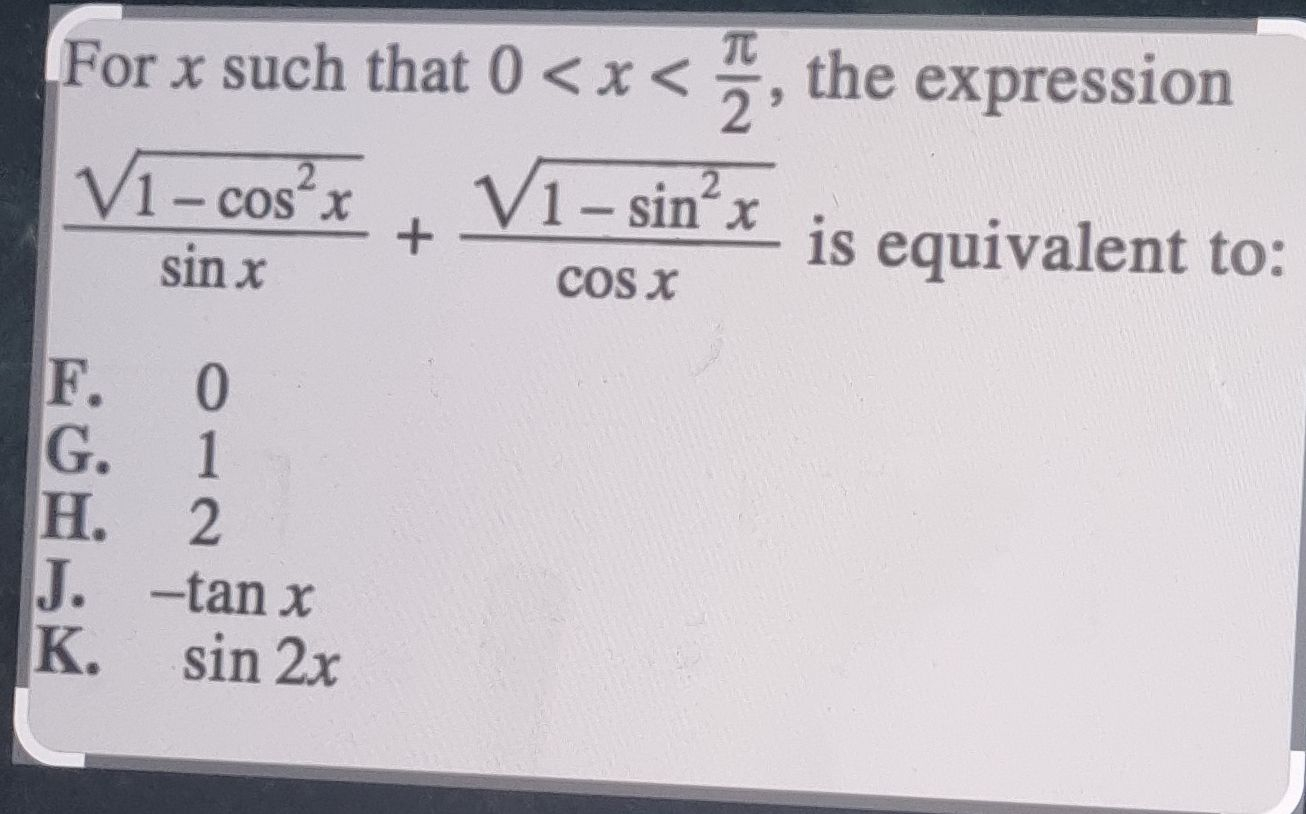Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

For
x such that
0 < x < (pi)/(2), the expression
(sqrt(1-cos^(2)x))/(sin x)+(sqrt(1-sin^(2)x))/(cos x) is equivalent to:
F. 0
G. 1
H. 2
J.
-tan x
K.
sin 2x

For $x$ such that $0<x<\frac{\pi}{2}$ , the expression $\frac{\sqrt{1-\cos ^{2} x}}{\sin x}+\frac{\sqrt{1-\sin ^{2} x}}{\cos x}$ is equivalent to: $\newline$ F. $0$ $\newline$ G. $1$ $\newline$ H. $2$ $\newline$ J. $-\tan x$ $\newline$ K. $\sin 2 x$

View step-by-step help

View step-by-step help

Function transformation rules

Full solution

Q. For

x

such that

0<x<\frac{\pi}{2}

, the expression

\frac{\sqrt{1-\cos ^{2} x}}{\sin x}+\frac{\sqrt{1-\sin ^{2} x}}{\cos x}

is equivalent to:

\newline

F.

0

\newline

G.

1

\newline

H.

2

\newline

J.

-\tan x

\newline

K.

\sin 2 x

Recognize Trigonometric Identities: Recognize that the expressions under the square roots are trigonometric identities. The identity $\sin^2(x) + \cos^2(x) = 1$ can be rearranged to $1 - \cos^2(x) = \sin^2(x)$ and $1 - \sin^2(x) = \cos^2(x)$ .
Substitute Identities: Substitute the identities into the original expression to simplify it. This gives us $(\sqrt{\sin^2(x)})/(\sin x) + (\sqrt{\cos^2(x)})/(\cos x)$ .
Simplify Square Roots: Since we are given that $0 < x < \frac{\pi}{2}$ , both $\sin x$ and $\cos x$ are positive in this range. Therefore, we can simplify $\sqrt{\sin^2(x)}$ to $\sin x$ and $\sqrt{\cos^2(x)}$ to $\cos x$ .
Combine Terms: After simplification, the expression becomes $\frac{\sin x}{\sin x} + \frac{\cos x}{\cos x}$ , which simplifies to $1 + 1$ .
Final Result: Adding the two terms together, we get $1 + 1 = 2$ .

More problems from Function transformation rules

Question

g(x)

g(x)

is the reflection across the x-axis of

f(x)=9|x+2|-4

\newline

\newline

\text{}(A)g(x) = 9|x+2| - 4\text{]}

\newline

\text{}(B)g(x) = 9|x-2| - 4\text{]}

\newline

\text{}(C)g(x)=-9|x-2| +4\text{]}

\newline

\text{(D)}g(x) = -9|x + 2| + 4\text{]}

Posted 2 months ago

Question

What does the transformation

f(x) \mapsto f(x - 4)

do to the graph of

f(x)

\newline

\newline

\text{translates it } 4 \text{ units right}

\newline

\text{translates it } 4 \text{ units down}

\newline

\text{translates it } 4 \text{ units left}

\newline

\text{translates it } 4 \text{ units up}

Posted 2 months ago

Question

What does the transformation

f(x) \mapsto f(4x)

do to the graph of

f(x)

\newline

\newline

[A] stretches it vertically

\newline

[B] stretches it horizontally

\newline

[C]shrinks it horizontally

\newline

[D]shrinks it vertically

Posted 1 month ago

Question

g(x)

g(x)

is the translation

9

f(x) = 10x + 8

\newline

\newline

g(x) = 10x - 82

\newline

g(x) = 10x + 98

\newline

g(x) = 10x - 1

\newline

g(x) = 10x + 17

Posted 2 months ago

Question

What kind of transformation converts the graph of

f(x) = -3x^2 - 4

into the graph of

g(x) = -3x^2 + 6

\newline

\newline

\text{[A]translation 10 units up}

\newline

\text{[B]translation 10 units down}

\newline

\text{[C]translation 10 units left}

\newline

\text{[D]translation 10 units right}

Posted 1 month ago

Question

y=x^{2}

is scaled vertically by a factor of

7

. What is the equation of the new parabola?

\newline

y=

Posted 4 months ago

Question

y=x^{2}

is shifted down by

6

units and to the right by

5

\newline

What is the equation of the new parabola?

\newline

y=

Posted 4 months ago

Question

y=x^{2}

is shifted up by

2

units and to the right by

3

\newline

What is the equation of the new parabola?

\newline

y=

Posted 1 month ago

Question

y=x^{2}

is reflected across the

x

-axis and then scaled vertically by a factor of

5

\newline

What is the equation of the new parabola?

\newline

y=\square

Posted 2 months ago

Question

y=x^{2}

is scaled vertically by a factor of

\frac{1}{10}

\newline

What is the equation of the new parabola?

\newline

y=

Posted 3 months ago