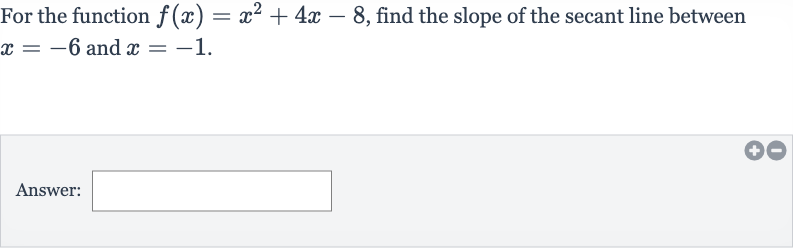
For the function f(x)=x^(2)+4x-8, find the slope of the secant line between x=-6 and x=-1. Answer:

Question

For the function  f(x)=x^(2)+4x-8, find the slope of the secant line between  x=-6 and  x=-1. Answer:

Bytelearn · Accepted Answer

Slope Formula: To find the slope of the secant line between two points on a function, we use the formula for slope, which is the change in y-values divided by the change in x-values. This is also known as the difference quotient. The formula is (f(x2) - f(x1)) / (x2 - x1), where x1 and x2 are the x-values of the two points.Find f(-6): First, we need to find the y-value for x = -6 by substituting -6 into the function f(x). So, f(-6) = (-6)^2 + 4(-6) - 8.Calculate f(-6): Calculating f(-6) gives us f(-6) = 36 - 24 - 8 = 4.Find f(-1): Next, we need to find the y-value for x = -1 by substituting -1 into the function f(x). So, f(-1) = (-1)^2 + 4(-1) - 8.Calculate f(-1): Calculating f(-1) gives us f(-1) = 1 - 4 - 8 = -11.Identify Two Points: Now we have the two points on the function: (-6, f(-6)) = (-6, 4) and (-1, f(-1)) = (-1, -11). We can use these points to find the slope of the secant line.Calculate Slope: The slope of the secant line is (f(-1) - f(-6)) / (-1 - (-6)) = (-11 - 4) / (-1 + 6).Calculating the slope gives us (-11 - 4) / (5) = -15 / 5 = -3.

For the function $f(x)=x^{2}+4 x-8$ , find the slope of the secant line between $x=-6$ and $x=-1$ . $\newline$ Answer:

Full solution

More problems from Find the roots of factored polynomials

Related topics

For the function f(x)=x2+4x−8 f(x)=x^{2}+4 x-8 f(x)=x2+4x−8, find the slope of the secant line between x=−6 x=-6 x=−6 and x=−1 x=-1 x=−1.\newlineAnswer:

For the function $f(x)=x^{2}+4 x-8$ , find the slope of the secant line between $x=-6$ and $x=-1$ . $\newline$ Answer: