Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

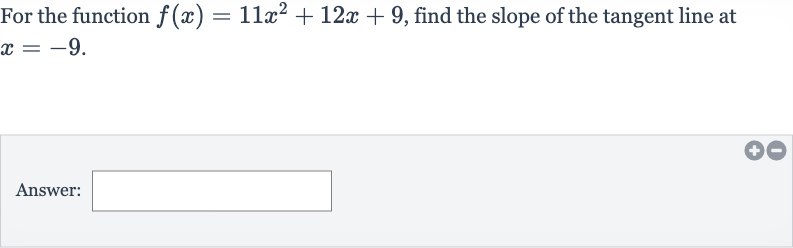
For the function
f(x)=11x^(2)+12 x+9, find the slope of the tangent line at
x=-9.
Answer:

For the function $f(x)=11 x^{2}+12 x+9$ , find the slope of the tangent line at $x=-9$ . $\newline$ Answer:

View step-by-step help

View step-by-step help

Find the slope of a tangent line using limits

Full solution

Q. For the function

f(x)=11 x^{2}+12 x+9

, find the slope of the tangent line at

x=-9

.

\newline

Answer:

Calculate Derivative: To find the slope of the tangent line to the function at a specific point, we need to calculate the derivative of the function, which gives us the slope of the tangent line at any point $x$ .
Evaluate at $x = -9$ : The derivative of $f(x) = 11x^2 + 12x + 9$ with respect to $x$ is $f'(x) = 22x + 12$ .
Substitute $x = -9$ : Now we need to evaluate the derivative at $x = -9$ to find the slope of the tangent line at that point.
Calculate $f'(-9)$ : Substitute $x = -9$ into the derivative to get $f'(-9) = 22(-9) + 12$ .
Simplify Expression: Calculate the value of $f'(-9)$ which is $22(-9) + 12 = -198 + 12$ .
Simplify Expression: Calculate the value of $f'(-9)$ which is $22(-9) + 12 = -198 + 12$ .Simplify the expression to get the final value of the slope at $x = -9$ , which is $-198 + 12 = -186$ .

More problems from Find the slope of a tangent line using limits

Question

Consider the curve given by the equation

x y^{2}+5 x y=50

. It can be shown that

\frac{d y}{d x}=\frac{-y(y+5)}{x(2 y+5)} \text {. }

\newline

Write the equation of the vertical line that is tangent to the curve.

Posted 1 month ago

Question

The rate of change

\frac{d P}{d t}

of the number of algae in a tank is modeled by the following differential equation:

\newline

\frac{d P}{d t}=\frac{2317}{10614} P\left(1-\frac{P}{662}\right)

\newline

t=0

, the number of algae in the tank is

174

and is increasing at a rate of

28

algae per minute. At what value of

P

P(t)

growing the fastest?

\newline

Posted 2 months ago

Question

The rate of change

\frac{d P}{d t}

of the number of bacteria in a tank is modeled by the following differential equation:

\newline

\frac{d P}{d t}=\frac{2}{9849} P(598-P)

\newline

t=0

, the number of bacteria in the tank is

196

and is increasing at a rate of

16

bacteria per minute. At what value of

P

does the graph of

P(t)

have an inflection point?

\newline

Posted 2 months ago

Question

The rate of change

\frac{d P}{d t}

of the number of people infected by a disease is modeled by the following differential equation:

\newline

\frac{d P}{d t}=\frac{45}{125404} P(800-P)

\newline

t=0

, the number of people infected by the disease is

214

and is increasing at a rate of

45

people per hour. What is the limiting value for the total number of people infected by the disease as time increases?

\newline

Posted 2 months ago

Question

Which of the following is a correct interpretation of the expression

\newline

-4+13

\newline

1

\newline

(A) The number that is

4

-13

on the number line

\newline

(B) The number that is

4

to the right of

-13

on the number line

\newline

(C) The number that is

13

-4

on the number line

\newline

(D) The number that is

13

to the right of

-4

on the number line

Posted 2 months ago

Question

f

f(x)=x^{3}+2 \sin (3 x-3)

. Use a calculator to write the equation of the line tangent to the graph of

f

x=0.5

. You should round all decimals to

3

\newline

Posted 2 months ago

Question

f

f(x)=x^{2}-2 x+3 \cos \left(x^{2}-x\right)

. Use a calculator to write the equation of the line tangent to the graph of

f

x=-2.5

. You should round all decimals to

3

\newline

Posted 2 months ago

Question

f

f(x)=x^{2}+x-2 \sin (2 x)

. Use a calculator to write the equation of the line tangent to the graph of

f

x=3

. You should round all decimals to

3

\newline

Posted 2 months ago

Question

f

f(x)=x^{3}+\cos \left(2 x^{2}+5\right)

. Use a calculator to write the equation of the line tangent to the graph of

f

x=1

. You should round all decimals to

3

\newline

Posted 2 months ago

Question

f

f(x)=x^{3}+3-5 \sin \left(x^{2}\right)

. Use a calculator to write the equation of the line tangent to the graph of

f

x=1

. You should round all decimals to

3

\newline

Posted 2 months ago