AI tutor
Full solution
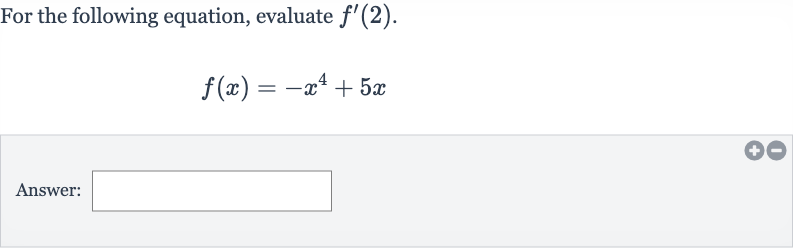
Q. For the following equation, evaluate .Answer:
- Identify Function: Given the function , we need to find the derivative of the function, which is denoted by . The derivative of a function gives us the rate at which the function's value changes at any given point.
- Apply Power Rule: To find , we will use the power rule for differentiation, which states that the derivative of with respect to is . We will apply this rule to each term in the function separately.
- Combine Derivatives: The derivative of the first term with respect to is (using the power rule). The derivative of the second term with respect to is (since the derivative of is and is a constant).
- Evaluate at : Combining the derivatives of both terms, we get .
- Calculate Final Value: Now we need to evaluate at . We substitute with in the derivative we found: .
- Calculate Final Value: Now we need to evaluate at . We substitute with in the derivative we found: . Calculating the value, .
More problems from Evaluate expression when a complex numbers and a variable term is given
QuestionGet tutor help
QuestionGet tutor help