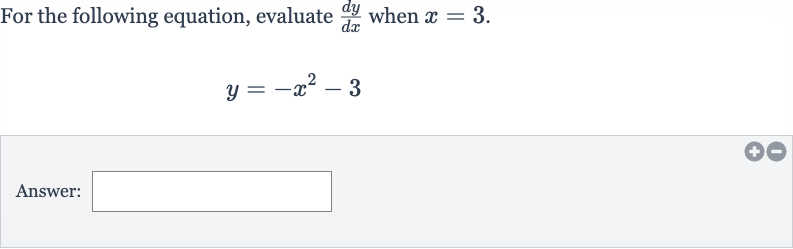Full solution
Q. For the following equation, evaluate when .Answer:
- Identify function: Identify the function to differentiate.We are given the function and we need to find its derivative with respect to .
- Differentiate with respect to x: Differentiate the function with respect to x.The derivative of with respect to , denoted as , is found by differentiating each term of the function separately.The derivative of with respect to is , and the derivative of a constant like is .
- Evaluate at : Evaluate the derivative at . Substitute into the derivative to find the slope of the tangent line to the curve at that point. at is . at =
More problems from Composition of linear and quadratic functions: find a value
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help