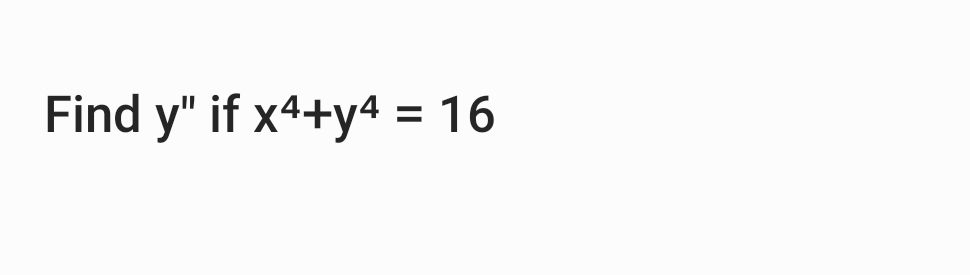Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find
y^('') if
x^(4)+y^(4)=16

Find $y^{\prime \prime}$ if $x^{4}+y^{4}=16$

View step-by-step help

View step-by-step help

Composition of linear and quadratic functions: find a value

Full solution

Q. Find

y^{\prime \prime}

if

x^{4}+y^{4}=16

Differentiate Equation: Differentiate both sides of the equation with respect to x. $\newline$ Given: $x^4 + y^4 = 16$ $\newline$ Differentiate: $\frac{d}{dx}(x^4) + \frac{d}{dx}(y^4) = \frac{d}{dx}(16)$ $\newline$ Using the chain rule on $y^4$ : $4x^3 + 4y^3 \frac{dy}{dx} = 0$
Solve for dy/dx: Solve for $\frac{dy}{dx}$ (first derivative of y). $\newline$ Rearrange the differentiated equation: $4y^3 \frac{dy}{dx} = -4x^3$ $\newline$ $\frac{dy}{dx} = -\frac{x^3}{y^3}$
Second Derivative of y: Differentiate $\frac{dy}{dx}$ again to find $\frac{d^2y}{dx^2}$ (second derivative of y). $\newline$ Differentiate: $\frac{d}{dx}\left(-\frac{x^3}{y^3}\right)$ $\newline$ Using the quotient rule: $\frac{d^2y}{dx^2} = \frac{-3x^2y^3 - (-x^3)(3y^2)\frac{dy}{dx}}{y^6}$ $\newline$ Substitute $\frac{dy}{dx} = -\frac{x^3}{y^3}$ into the equation. $\newline$ $\frac{d^2y}{dx^2} = \frac{-3x^2y^3 + 3x^3y^2 \left(-\frac{x^3}{y^3}\right)}{y^6}$ $\newline$ Simplify: $\frac{d^2y}{dx^2} = \frac{-3x^2y^3 - 3x^6}{y^6}$

More problems from Composition of linear and quadratic functions: find a value

Question

Find the inverse of the function.

y = x + 3

Write your answer in the form

ax + b

. Simplify any fractions.

y =

Posted 2 months ago

Question

(r \circ s)(x)

\newline

3

\newline

2

5

\newline

Write your answer as a polynomial in simplest form.

\newline

(r \circ s)(x) =

Posted 1 month ago

Question

(f + g)(x)

\newline

f(x) = -3x

\newline

g(x) = 3x + 1

\newline

\newline

Write your answer as a polynomial or a rational function in simplest form.

\newline

\underline{\hspace{3cm}}

\newline

Posted 1 month ago

Question

(f * g)(x)

\newline

f(x) = -x + 4

\newline

g(x) = 4x

\newline

\newline

Write your answer as a polynomial or a rational function in simplest form.

\newline

\underline{\hspace{3em}}

\newline

Posted 1 month ago

Question

What is the domain of

\left(\frac{f}{g}\right)(x)

\newline

f(x) = 2x

\newline

g(x) = -5x + 3

\newline

\newline

[\text{A]All real numbers}

\newline

[\text{B]All real numbers except } \frac{3}{5}

\newline

[\text{C]All real numbers except } -\frac{3}{5}

\newline

[\text{D]All real numbers except } \frac{5}{3}

Posted 2 months ago

Question

Find the inverse of the function.

\newline

-3x

\newline

Write your answer in the form

ax + b

. Simplify any fractions.

\newline

Posted 1 month ago

Question

(f \circ g)(0)

\newline

f(x) = 6x

\newline

g(x) = x^2 + 4x

\newline

(f \circ g)(0) =

Posted 1 month ago

Question

(f \circ g)(x)

\newline

f(x) = x^2 + 5

\newline

g(x) = 4x

\newline

Write your answer as a polynomial in simplest form.

\newline

(f \circ g)(x) =

Posted 1 month ago

Question

f(x)

the inverse function of

g(x)

\newline

f(x) = x

\newline

g(x) = -4x

\newline

\newline

\text{[yes]}

\newline

\text{[no]}

Posted 1 month ago

Question

(f * g)(x)

f(x) = 3x^2 + 9x

g(x) = 3x

Write your answer as a polynomial or a rational function in simplest form. ______

Posted 2 months ago