Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

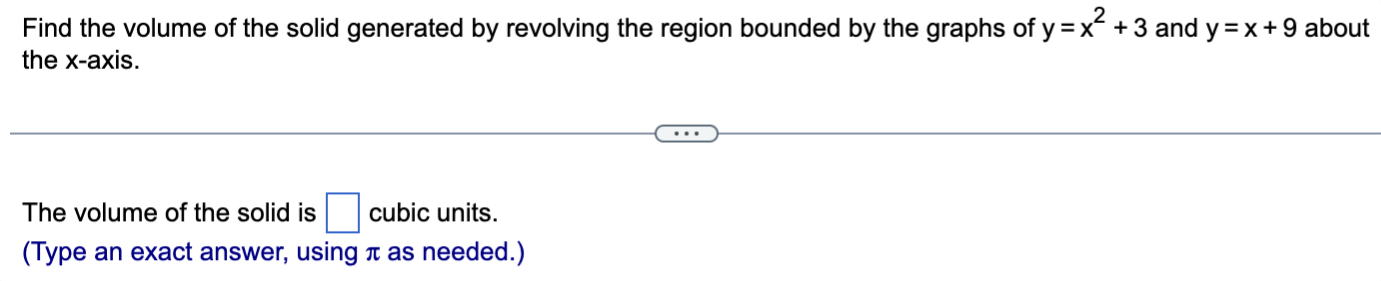
Find the volume of the solid generated by revolving the region bounded by the graphs of
y=x^(2)+3 and
y=x+9 about the
x-axis.
The volume of the solid is
◻ cubic units.
(Type an exact answer, using
pi as needed.)

Find the volume of the solid generated by revolving the region bounded by the graphs of $y=x^{2}+3$ and $y=x+9$ about the $x$ -axis. $\newline$ The volume of the solid is $\square$ cubic units. $\newline$ (Type an exact answer, using $\pi$ as needed.)

View step-by-step help

View step-by-step help

Conjugate root theorems

Full solution

Q. Find the volume of the solid generated by revolving the region bounded by the graphs of

y=x^{2}+3

and

y=x+9

about the

x

-axis.

\newline

The volume of the solid is

\square

cubic units.

\newline

(Type an exact answer, using

\pi

as needed.)

Identify bounds of integration: Identify the bounds of integration by setting the equations equal to each other: $x^2 + 3 = x + 9$ . Solve for $x$ : $\newline$ $x^2 - x - 6 = 0$ $\newline$ $(x - 3)(x + 2) = 0$ $\newline$ $x = 3, x = -2$
Set up integral for volume: Set up the integral for the volume using the washer method, where the outer radius $R(x)$ is $x+9$ and the inner radius $r(x)$ is $x^2+3$ : $\text{Volume} = \pi \int_{x=-2}^{x=3} [(x+9)^2 - (x^2+3)^2] \, dx$
Expand and simplify integrand: Expand the squares and simplify the integrand: $\newline$ $(x+9)^2 = x^2 + 18x + 81$ $\newline$ $(x^2+3)^2 = x^4 + 6x^2 + 9$ $\newline$ Integrand: $(x^2 + 18x + 81) - (x^4 + 6x^2 + 9)$ $\newline$ Simplify: $-x^4 - 4x^2 + 18x + 72$
Integrate function: Integrate the function from $-2$ to $3$ : $\int_{-2}^{3}[-x^4 - 4x^2 + 18x + 72] dx$ = $\left(\frac{-1}{5}x^5 - \frac{4}{3}x^3 + 9x^2 + 72x\right)$ from $-2$ to $3$ = $\left(\frac{-1}{5}(3)^5 - \frac{4}{3}(3)^3 + 9(3)^2 + 72(3)\right) - \left(\frac{-1}{5}(-2)^5 - \frac{4}{3}(-2)^3 + 9(-2)^2 + 72(-2)\right)$ = $-48.6 - 36 + 81 + 216$ - $6.4 + 10.67 + 36 - 144$ = $212.4$ - $-91.07$ = $303.47$

More problems from Conjugate root theorems

Question

Find the degree of this polynomial.

\newline

`5b^{10} + 3b^3`

\newline

Posted 3 months ago

Question

\newline

(9a + 5) - (2a + 4)

\newline

Posted 3 months ago

Question

Find the product. Simplify your answer.

\newline

-3v^2(v^2 - 9)

\newline

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

(v - 3)(4v + 1)

\newline

Posted 3 months ago

Question

Find the square. Simplify your answer.

\newline

(3y + 2)^2

\newline

Posted 3 months ago

Question

Divide. If there is a remainder, include it as a simplified fraction.

\newline

(24t^2 + 36t) \div 6t

\newline

Posted 2 months ago

Question

Is the function

q(x) = x^6 - 9

even, odd, or neither?

\newline

\newline

\text{[[even][odd][neither]]}

Posted 3 months ago

Question

Find the product. Simplify your answer.

\newline

-3q^2(-3q^2 + q)

\newline

Posted 3 months ago

Question

Find the product. Simplify your answer.

\newline

(r + 3)(4r + 2)

\newline

Posted 3 months ago

Question

Find the roots of the factored polynomial.

\newline

(x + 7)(x + 4)

\newline

Write your answer as a list of values separated by commas.

\newline

x =

Posted 3 months ago