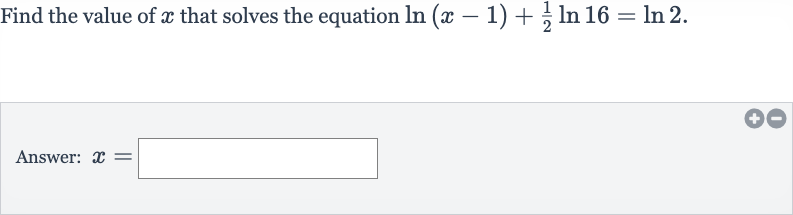
Find the value of x that solves the equation ln(x-1)+(1)/(2)ln 16=ln 2. Answer: x=

Question

Find the value of  x that solves the equation  ln(x-1)+(1)/(2)ln 16=ln 2. Answer:  x=

Bytelearn · Accepted Answer

Simplify equation: First, we need to simplify the equation using properties of logarithms. The equation is ln(x-1) + (1/2)ln 16 = ln 2. We know that (1/2)ln 16 can be simplified because ln 16 is the natural log of 2 to the power of 4, so (1/2)ln 16 is the same as ln 16^(1/2) or ln 4.Rewrite with simplification: Now we rewrite the equation using the simplification from the previous step: ln(x-1) + ln 4 = ln 2.Combine left side: Using the property of logarithms that ln a + ln b = ln(ab), we can combine the left side of the equation: ln((x-1)*4) = ln 2.Simplify left side: Simplify the left side of the equation to get ln(4x-4) = ln 2.Set up equation: Since the natural log function is one-to-one, if ln(4x-4) = ln 2, then 4x-4 must be equal to 2. We can now solve for x by setting 4x-4 equal to 2.Isolate x term: Add 4 to both sides of the equation to isolate the term with x: 4x-4+4 = 2+4, which simplifies to 4x = 6.Solve for x: Divide both sides of the equation by 4 to solve for x: 4x/4 = 6/4, which simplifies to x = 6/4 or x = 1.5.

Find the value of $x$ that solves the equation $\ln (x-1)+\frac{1}{2} \ln 16=\ln 2$ . $\newline$ Answer: $x=$

Full solution

More problems from Find the roots of factored polynomials

Related topics

Find the value of x x x that solves the equation ln⁡(x−1)+12ln⁡16=ln⁡2 \ln (x-1)+\frac{1}{2} \ln 16=\ln 2 ln(x−1)+21​ln16=ln2.\newlineAnswer: x= x= x=

Find the value of $x$ that solves the equation $\ln (x-1)+\frac{1}{2} \ln 16=\ln 2$ . $\newline$ Answer: $x=$