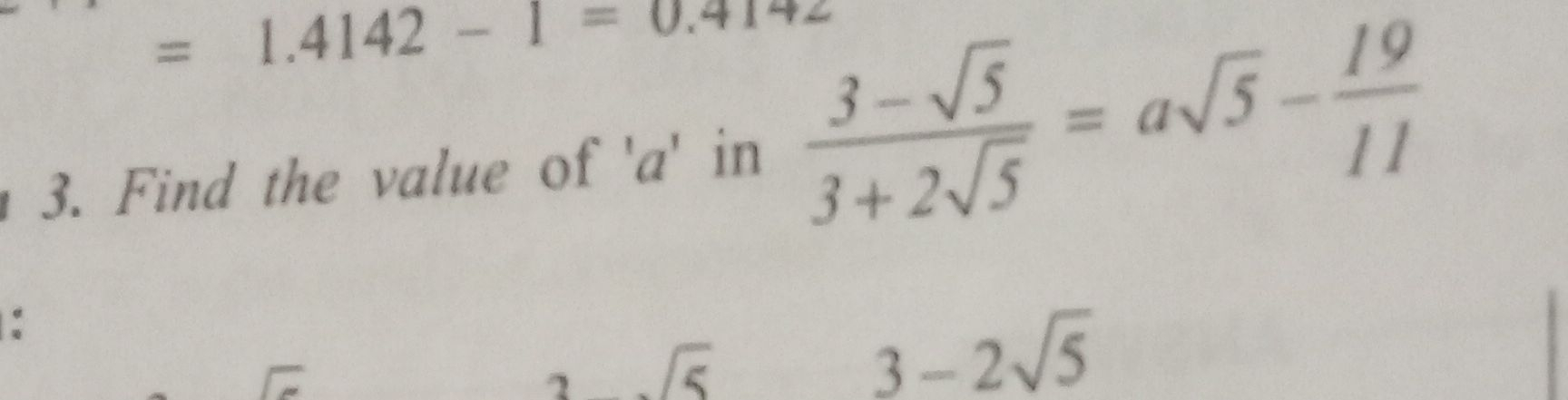Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the value of ' a ' in (3-sqrt5)/(3+2sqrt5)=asqrt5-(19)/(11)

Find the value of ' a a ' in 3−53+25=a5−1911 \frac{3-\sqrt{5}}{3+2 \sqrt{5}}=a \sqrt{5}-\frac{19}{11}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Composition of linear functions: find a valueright chevron icon

Full solution

Q. Find the value of ' a a ' in 3−53+25=a5−1911 \frac{3-\sqrt{5}}{3+2 \sqrt{5}}=a \sqrt{5}-\frac{19}{11}
  1. Rationalize Denominator: First, let's rationalize the denominator of the left side of the equation by multiplying both the numerator and denominator by the conjugate of the denominator.\newline(3−5)/(3+25)×(3−25)/(3−25)(3-\sqrt{5})/(3+2\sqrt{5}) \times (3-2\sqrt{5})/(3-2\sqrt{5})
  2. Multiply Numerators and Denominators: Now, multiply the numerators and the denominators.\newlineNumerator: (3−5)(3−25)(3-\sqrt{5})(3-2\sqrt{5})\newlineDenominator: (3+25)(3−25)(3+2\sqrt{5})(3-2\sqrt{5})
  3. Expand Using FOIL Method: Use the FOIL method to expand the numerator and denominator.\newlineNumerator: 3×3−3×25−5×3+5×253\times3 - 3\times2\sqrt{5} - \sqrt{5}\times3 + \sqrt{5}\times2\sqrt{5}\newlineDenominator: 3×3−3×25+25×3−25×253\times3 - 3\times2\sqrt{5} + 2\sqrt{5}\times3 - 2\sqrt{5}\times2\sqrt{5}
  4. Simplify Expressions: Simplify the expressions.\newlineNumerator: 9−65−35+2⋅59 - 6\sqrt{5} - 3\sqrt{5} + 2\cdot 5\newlineDenominator: 9−65+65−2⋅59 - 6\sqrt{5} + 6\sqrt{5} - 2\cdot 5
  5. Combine Like Terms: Combine like terms.\newlineNumerator: 9+10−959 + 10 - 9\sqrt{5}\newlineDenominator: 9−109 - 10
  6. Further Simplify Terms: Simplify the terms further.\newlineNumerator: 19−9519 - 9\sqrt{5}\newlineDenominator: −1-1
  7. Divide Numerator by Denominator: Divide the numerator by the denominator.\newline(19−95)/−1=−19+95(19 - 9\sqrt{5}) / -1 = -19 + 9\sqrt{5}
  8. Set Equal to Right Side: Now we have the left side of the equation simplified to −19+95-19 + 9\sqrt{5}. Set this equal to the right side of the original equation. −19+95=a5−1911-19 + 9\sqrt{5} = a\sqrt{5} - \frac{19}{11}
  9. Find 'a': To find 'a', we need to compare the coefficients of 5\sqrt{5} on both sides of the equation.9=a9 = a

More problems from Composition of linear functions: find a value

Question
Find the inverse of the function. y=x+3 y = x + 3 Write your answer in the form ax+b ax + b . Simplify any fractions. y= y = _____
Get tutor helpright-arrow

Posted 2 months ago

Question
Find (r∘s)(x)(r \circ s)(x).\newliner(x) = 33x\newlines(x) = 22x + 55\newlineWrite your answer as a polynomial in simplest form.\newline(r∘s)(x)=(r \circ s)(x) = ____
Get tutor helpright-arrow

Posted 1 month ago

Question
What is (f+g)(x)(f + g)(x)?\newlinef(x)=−3xf(x) = -3x\newlineg(x)=3x+1g(x) = 3x + 1\newline\newlineWrite your answer as a polynomial or a rational function in simplest form.\newline‾\underline{\hspace{3cm}}\newline
Get tutor helpright-arrow

Posted 1 month ago

Question
What is (f∗g)(x)(f * g)(x)?\newlinef(x)=−x+4f(x) = -x + 4\newlineg(x)=4xg(x) = 4x\newline\newlineWrite your answer as a polynomial or a rational function in simplest form.\newline‾\underline{\hspace{3em}}\newline
Get tutor helpright-arrow

Posted 1 month ago

Question
What is the domain of (fg)(x)\left(\frac{f}{g}\right)(x)?\newlinef(x)=2xf(x) = 2x\newlineg(x)=−5x+3g(x) = -5x + 3\newlineChoices:\newline[A]All real numbers[\text{A]All real numbers}\newline[B]All real numbers except 35[\text{B]All real numbers except } \frac{3}{5}\newline[C]All real numbers except −35[\text{C]All real numbers except } -\frac{3}{5}\newline[D]All real numbers except 53[\text{D]All real numbers except } \frac{5}{3}
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the inverse of the function.\newliney = −3x-3x \newlineWrite your answer in the form ax+bax + b. Simplify any fractions.\newliney = ______
Get tutor helpright-arrow

Posted 1 month ago

Question
Find (f∘g)(0)(f \circ g)(0).\newlinef(x)=6xf(x) = 6x\newlineg(x)=x2+4xg(x) = x^2 + 4x\newline(f∘g)(0)=(f \circ g)(0) = ____
Get tutor helpright-arrow

Posted 1 month ago

Question
Find (f∘g)(x)(f \circ g)(x).\newlinef(x)=x2+5f(x) = x^2 + 5\newlineg(x)=4xg(x) = 4x\newlineWrite your answer as a polynomial in simplest form.\newline(f∘g)(x)=(f \circ g)(x) = ______
Get tutor helpright-arrow

Posted 1 month ago

Question
Is f(x) f(x) the inverse function of g(x) g(x) ?\newlinef(x)=x f(x) = x \newlineg(x)=−4x g(x) = -4x \newlineChoices:\newline[yes] \text{[yes]} \newline[no] \text{[no]}
Get tutor helpright-arrow

Posted 1 month ago

Question
What is (f∗g)(x)(f * g)(x)? f(x)=3x2+9xf(x) = 3x^2 + 9x g(x)=3xg(x) = 3x Write your answer as a polynomial or a rational function in simplest form. ______
Get tutor helpright-arrow

Posted 2 months ago

View all (36)