AI tutor
Full solution
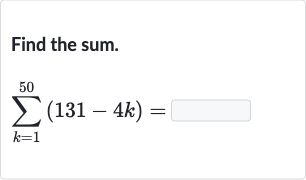
Q. Find the sum.
- Understand the series: Understand the series and its general term.The series is the sum of terms of the form where takes on integer values from to . We need to find the sum of all these terms.
- Calculate first term: Calculate the first term of the series.Substitute into the general term to find the first term.First term =
- Calculate last term: Calculate the last term of the series.Substitute into the general term to find the last term.Last term =
- Calculate sum of series: Calculate the sum of the arithmetic series.The sum of an arithmetic series can be found using the formula:Sum where is the number of terms. In this case, .Sum
- Perform calculations: Perform the calculations to find the sum.Sum =
More problems from Composition of linear and quadratic functions: find a value
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help