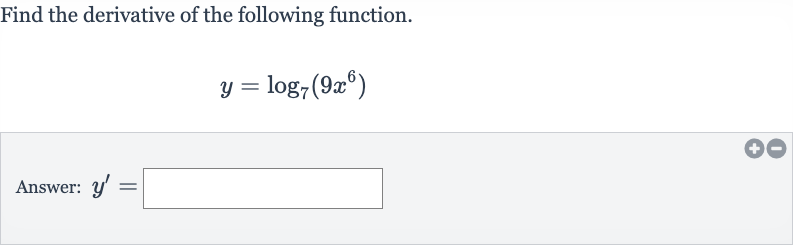
Find the derivative of the following function. y=log_(7)(9x^(6)) Answer: y^(')=

Question

Find the derivative of the following function.  y=log_(7)(9x^(6)) Answer:  y^(')=

Bytelearn · Accepted Answer

Understand function and derivative: Understand the function and the type of derivative to find. We need to find the derivative of the function y with respect to x, where y is a logarithm with base 7 of the function 9x^6. We will use the chain rule and the formula for the derivative of a logarithm with an arbitrary base.Apply chain rule and formula: Apply the chain rule and the logarithmic derivative formula. The chain rule states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function. The derivative of log_b(u) with respect to u is 1/(u * ln(b)), where b is the base of the logarithm and ln is the natural logarithm.Calculate inner function derivative: Calculate the derivative of the inner function 9x^6 with respect to x. The inner function is 9x^6, and its derivative with respect to x is 54x^5 (using the power rule: d/dx [ax^n] = n*ax^(n-1)).Combine using chain rule: Combine the results using the chain rule. The derivative of y with respect to x is the derivative of the outer function (log_7(u)) times the derivative of the inner function (9x^6). Using the formula from Step 2 and the result from Step 3, we get: y' = (1/(9x^6 * ln(7))) * 54x^5Simplify the expression: Simplify the expression. We can simplify the expression by canceling out an x^5 from the numerator and denominator, and simplifying the constants: y' = (54/(9 * ln(7))) * x^(5-6) y' = (6/(ln(7))) * x^(-1) y' = 6x^(-1) / ln(7)

Find the derivative of the following function. $\newline$ $y=\log _{7}\left(9 x^{6}\right)$ $\newline$ Answer: $y^{\prime}=$

Full solution

More problems from Quotient property of logarithms

Related topics

Find the derivative of the following function.\newliney=log⁡7(9x6) y=\log _{7}\left(9 x^{6}\right) y=log7​(9x6)\newlineAnswer: y′= y^{\prime}= y′=

Find the derivative of the following function. $\newline$ $y=\log _{7}\left(9 x^{6}\right)$ $\newline$ Answer: $y^{\prime}=$