Full solution
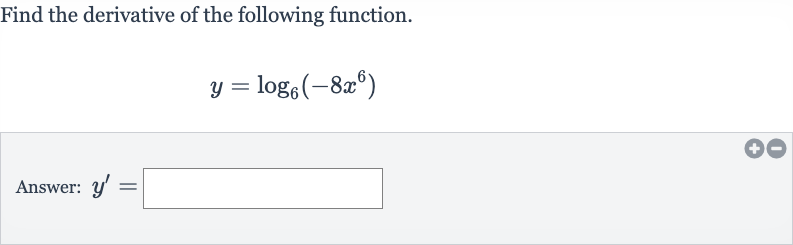
Q. Find the derivative of the following function.Answer:
- Understand and Apply Chain Rule: Understand the function and apply the chain rule.The function is a logarithmic function with base . To find the derivative, we need to use the chain rule, which states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function.
- Differentiate Outer Function: Differentiate the outer function.The outer function is , where . The derivative of with respect to is according to the logarithmic differentiation rule.
- Differentiate Inner Function: Differentiate the inner function.The inner function is . The derivative of with respect to is by using the power rule.
- Apply Chain Rule: Apply the chain rule.Now we multiply the derivative of the outer function by the derivative of the inner function to get the derivative of the composite function.
- Simplify Expression: Simplify the expression.We can simplify the expression by multiplying the constants and combining like terms.