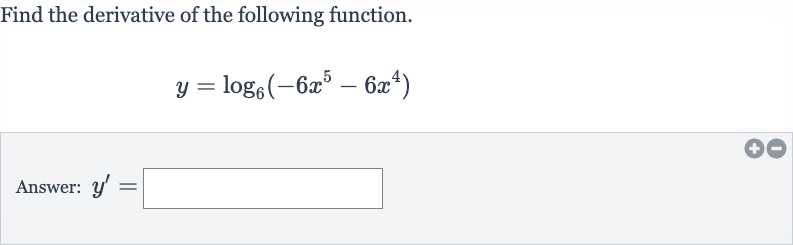
Find the derivative of the following function. y=log_(6)(-6x^(5)-6x^(4)) Answer: y^(')=

Question

Find the derivative of the following function.  y=log_(6)(-6x^(5)-6x^(4)) Answer:  y^(')=

Bytelearn · Accepted Answer

Identify Function and Derivative: Identify the function and the type of derivative to be found. We are given the function y=log_6(-6x^5-6x^4) and we need to find its derivative with respect to x.Apply Chain Rule for Logarithmic Differentiation: Apply the chain rule for logarithmic differentiation. The chain rule states that the derivative of log_b(u(x)) is (1/u(x)) * (du/dx), where b is the base of the logarithm and u(x) is the function inside the logarithm.Differentiate Inside Function: Differentiate the inside function -6x^5-6x^4 with respect to x. The derivative of -6x^5 is -30x^4 and the derivative of -6x^4 is -24x^3. So, the derivative of the inside function is -30x^4 - 24x^3.Apply Change of Base Formula: Apply the change of base formula for logarithms. The change of base formula is log_b(a) = log_c(a) / log_c(b), where c is a new base. We can use the natural logarithm (base e) for this purpose. So, y=log_6(-6x^5-6x^4) can be rewritten as y=(ln(-6x^5-6x^4))/(ln(6)).Differentiate Using Quotient Rule: Differentiate y with respect to x using the quotient rule. The quotient rule is (v * (du/dx) - u * (dv/dx)) / v^2, where u is the numerator and v is the denominator. Here, u = ln(-6x^5-6x^4) and v = ln(6). Since ln(6) is a constant, its derivative dv/dx is 0. The derivative of y is then (ln(6) * d/dx[ln(-6x^5-6x^4)] - ln(-6x^5-6x^4) * 0) / (ln(6))^2. Simplifying, we get y' = (1/ln(6)) * d/dx[ln(-6x^5-6x^4)].Substitute Derivative of Inside Function: Substitute the derivative of the inside function into the derivative of y. From Step 3, we have d/dx[ln(-6x^5-6x^4)] = (1/(-6x^5-6x^4)) * (-30x^4 - 24x^3). So, y' = (1/ln(6)) * (1/(-6x^5-6x^4)) * (-30x^4 - 24x^3).Simplify Derivative Expression: Simplify the expression for the derivative. y' = (1/ln(6)) * (-30x^4 - 24x^3) / (-6x^5-6x^4).Factor Out Common Terms: Factor out common terms and simplify further if possible. We can factor out -6x^3 from the numerator and denominator. y' = (1/ln(6)) * (-6x^3(5x + 4)) / (-6x^3(x + 1)). After canceling out -6x^3 from the numerator and denominator, we get: y' = (1/ln(6)) * (5x + 4) / (x + 1).

Find the derivative of the following function. $\newline$ $y=\log _{6}\left(-6 x^{5}-6 x^{4}\right)$ $\newline$ Answer: $y^{\prime}=$

Full solution

More problems from Quotient property of logarithms

Related topics

Find the derivative of the following function.\newliney=log⁡6(−6x5−6x4) y=\log _{6}\left(-6 x^{5}-6 x^{4}\right) y=log6​(−6x5−6x4)\newlineAnswer: y′= y^{\prime}= y′=

Find the derivative of the following function. $\newline$ $y=\log _{6}\left(-6 x^{5}-6 x^{4}\right)$ $\newline$ Answer: $y^{\prime}=$