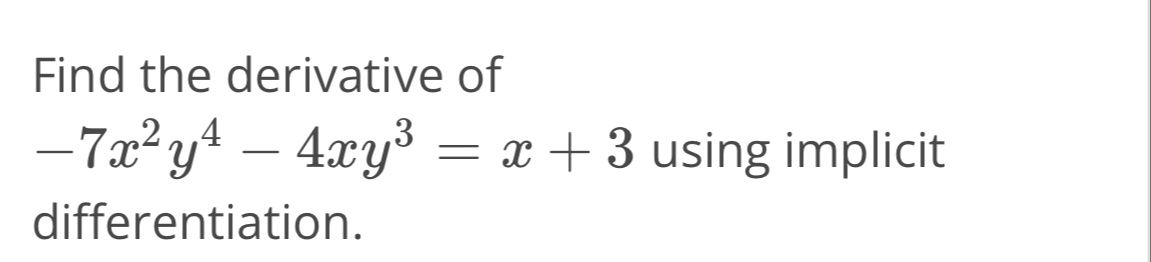Find the derivative of -7x^(2)y^(4)-4xy^(3)=x+3 using implicit differentiation.

Question

Find the derivative of  -7x^(2)y^(4)-4xy^(3)=x+3 using implicit differentiation.

Bytelearn · Accepted Answer

Differentiate with respect to x: Differentiate both sides of the equation with respect to x. We will use the product rule for differentiation, which states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function. We will also use the chain rule, which states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function. Differentiate the left side: d/dx(-7x^(2)y^(4)) = -7 * d/dx(x^(2)y^(4)) d/dx(-4xy^(3)) = -4 * d/dx(xy^(3)) Differentiate the right side: d/dx(x+3) = d/dx(x) + d/dx(3)Apply product rule: Apply the product rule to the terms involving both x and y. For -7x^(2)y^(4), we have two functions: x^(2) and y^(4). Their derivatives are 2x and 4y^(3)dy/dx, respectively, since y is a function of x and we are differentiating with respect to x. For -4xy^(3), we have two functions: x and y^(3). Their derivatives are 1 and 3y^(2)dy/dx, respectively. Now apply the product rule: d/dx(-7x^(2)y^(4)) = -7 * (2x * y^(4) + x^(2) * 4y^(3)dy/dx) d/dx(-4xy^(3)) = -4 * (1 * y^(3) + x * 3y^(2)dy/dx)Differentiate right side: Differentiate the right side of the equation. The derivative of x with respect to x is 1, and the derivative of a constant, 3, is 0. So, d/dx(x+3) = 1 + 0 = 1.Write down derivatives: Write down the derivatives we found in Steps 2 and 3. -7 * (2x * y^(4) + x^(2) * 4y^(3)dy/dx) - 4 * (y^(3) + x * 3y^(2)dy/dx) = 1Simplify equation: Simplify the equation by distributing the constants and combining like terms. -14x * y^(4) - 28x^(2) * y^(3)dy/dx - 4y^(3) - 12xy^(2)dy/dx = 1Isolate terms: Isolate terms involving dy/dx on one side of the equation and the rest on the other side. -28x^(2) * y^(3)dy/dx - 12xy^(2)dy/dx = 1 + 14x * y^(4) + 4y^(3)Factor out dy/dx: Factor out dy/dx from the left side of the equation. dy/dx(-28x^(2) * y^(3) - 12xy^(2)) = 1 + 14x * y^(4) + 4y^(3)Solve for dy/dx: Solve for dy/dx. dy/dx = (1 + 14x * y^(4) + 4y^(3)) / (-28x^(2) * y^(3) - 12xy^(2))

Find the derivative of $-7 x^{2} y^{4}-4 x y^{3}=x+3$ using implicit differentiation.

Full solution

More problems from Transformations of functions

Related topics

Find the derivative of −7x2y4−4xy3=x+3 -7 x^{2} y^{4}-4 x y^{3}=x+3 −7x2y4−4xy3=x+3 using implicit differentiation.

Find the derivative of $-7 x^{2} y^{4}-4 x y^{3}=x+3$ using implicit differentiation.