AI tutor
Full solution
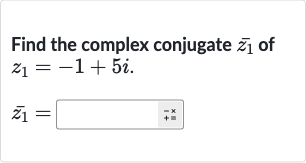
Q. Find the complex conjugate of .
- Identify parts of : Identify the real and imaginary parts of the complex number . In the complex number , is the real part and is the coefficient of the imaginary part . Real part: Imaginary part:
- Determine complex conjugate: Determine the complex conjugate of . The complex conjugate of a complex number is obtained by changing the sign of the imaginary part. Therefore, the complex conjugate of is . Complex conjugate:
More problems from Complex conjugates
QuestionGet tutor help
QuestionGet tutor help