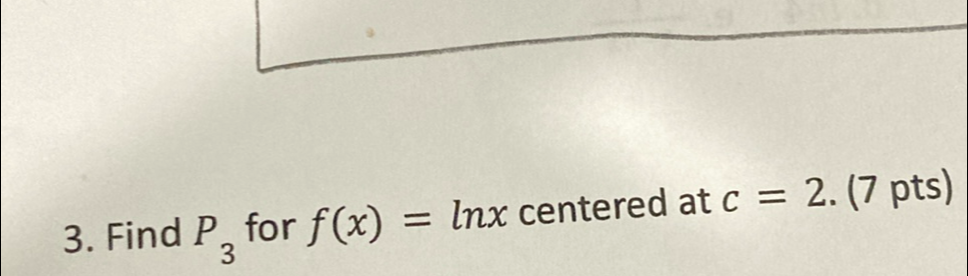Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find P_(3) for f(x)=ln x centered at c=2.

Find $P_{3}$ for $f(x)=\ln x$ centered at $c=2.$

View step-by-step help

View step-by-step help

Find values of derivatives using limits

Full solution

Q. Find

P_{3}

for

f(x)=\ln x

centered at

c=2.

Identify Function & Expansion Point: Identify the function and the point of expansion. $\newline$ We are given the function $f(x) = \ln(x)$ and we need to find the third-degree Taylor polynomial ( $P_3$ ) centered at $c = 2$ .
Calculate First Derivative: Calculate the first derivative of $f(x)$ . The first derivative of $f(x) = \ln(x)$ is $f'(x) = \frac{1}{x}$ . We evaluate this at $x = 2$ to get $f'(2) = \frac{1}{2}$ .
Calculate Second Derivative: Calculate the second derivative of $f(x)$ . $\newline$ The second derivative of $f'(x) = \frac{1}{x}$ is $f''(x) = -\frac{1}{x^2}$ . We evaluate this at $x = 2$ to get $f''(2) = -\frac{1}{4}$ .
Calculate Third Derivative: Calculate the third derivative of $f(x)$ . The third derivative of $f''(x) = -\frac{1}{x^2}$ is $f(x) = \frac{2}{x^3}$ . We evaluate this at $x = 2$ to get $f(2) = \frac{2}{8} = \frac{1}{4}$ .
Write Taylor Polynomial Formula: Write down the formula for the third-degree Taylor polynomial. $\newline$ The third-degree Taylor polynomial is given by: $\newline$ $P_3(x) = f(c) + f'(c)(x - c) + \frac{f''(c)(x - c)^2}{2!} + \frac{f(c)(x - c)^3}{3!}$
Substitute Values: Substitute the values into the Taylor polynomial formula. $\newline$ Using the values from the previous steps, we get: $\newline$ $P_3(x) = \ln(2) + \left(\frac{1}{2}\right)(x - 2) - \left(\frac{1}{4}\right)\frac{(x - 2)^2}{2!} + \left(\frac{1}{4}\right)\frac{(x - 2)^3}{3!}$
Simplify Polynomial: Simplify the polynomial. $\newline$ $P_3(x) = \ln(2) + \left(\frac{1}{2}\right)(x - 2) - \left(\frac{1}{8}\right)(x - 2)^2 + \left(\frac{1}{24}\right)(x - 2)^3$ $\newline$ This is the third-degree Taylor polynomial for $f(x) = \ln(x)$ centered at $c = 2$ .

More problems from Find values of derivatives using limits

Question

Consider the curve given by the equation

x y^{2}+5 x y=50

. It can be shown that

\frac{d y}{d x}=\frac{-y(y+5)}{x(2 y+5)} \text {. }

\newline

Write the equation of the vertical line that is tangent to the curve.

Posted 7 months ago

Question

What is the value of

\frac{d}{d x}\left(x^{-3}\right)

x=3

Posted 3 months ago

Question

The rate of change

\frac{d P}{d t}

of the number of algae in a tank is modeled by the following differential equation:

\newline

\frac{d P}{d t}=\frac{2317}{10614} P\left(1-\frac{P}{662}\right)

\newline

t=0

, the number of algae in the tank is

174

and is increasing at a rate of

28

algae per minute. At what value of

P

P(t)

growing the fastest?

\newline

Posted 9 months ago

Question

The rate of change

\frac{d P}{d t}

of the number of bacteria in a tank is modeled by the following differential equation:

\newline

\frac{d P}{d t}=\frac{2}{9849} P(598-P)

\newline

t=0

, the number of bacteria in the tank is

196

and is increasing at a rate of

16

bacteria per minute. At what value of

P

does the graph of

P(t)

have an inflection point?

\newline

Posted 9 months ago

Question

The rate of change

\frac{d P}{d t}

of the number of people infected by a disease is modeled by the following differential equation:

\newline

\frac{d P}{d t}=\frac{45}{125404} P(800-P)

\newline

t=0

, the number of people infected by the disease is

214

and is increasing at a rate of

45

people per hour. What is the limiting value for the total number of people infected by the disease as time increases?

\newline

Posted 9 months ago

Question

The exponential function

f

is graphed in the

x y

x

1, y

increases by a factor of

3

. Which of the following could be

f

\newline

1

\newline

f(x)=\left(\frac{1}{3}\right)^{x}

\newline

f(x)=\left(\frac{1}{3}\right)^{x}+3

\newline

f(x)=3^{x}+2

\newline

f(x)=2(3)^{x}

Posted 2 months ago

Question

Which of the following is a correct interpretation of the expression

\newline

-4+13

\newline

1

\newline

(A) The number that is

4

-13

on the number line

\newline

(B) The number that is

4

to the right of

-13

on the number line

\newline

(C) The number that is

13

-4

on the number line

\newline

(D) The number that is

13

to the right of

-4

on the number line

Posted 8 months ago

Question

f

f(x)=x^{3}+2 \sin (3 x-3)

. Use a calculator to write the equation of the line tangent to the graph of

f

x=0.5

. You should round all decimals to

3

\newline

Posted 9 months ago

Question

f

f(x)=x^{2}-2 x+3 \cos \left(x^{2}-x\right)

. Use a calculator to write the equation of the line tangent to the graph of

f

x=-2.5

. You should round all decimals to

3

\newline

Posted 9 months ago

Question

f

f(x)=x^{2}+x-2 \sin (2 x)

. Use a calculator to write the equation of the line tangent to the graph of

f

x=3

. You should round all decimals to

3

\newline

Posted 9 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant