Find $\lim _{x \rightarrow 5} \frac{x+2}{x^{2}-5}$ . $\newline$ Choose $1$ answer: $\newline$ (A) $-\frac{3}{25}$ $\newline$ (B) $\frac{7}{20}$ $\newline$ (C) $-\frac{7}{25}$ $\newline$ (D) The limit doesn't exist

Full solution

Q. Find

\lim _{x \rightarrow 5} \frac{x+2}{x^{2}-5}

\newline

Choose

1

answer:

\newline

(A)

-\frac{3}{25}

\newline

(B)

\frac{7}{20}

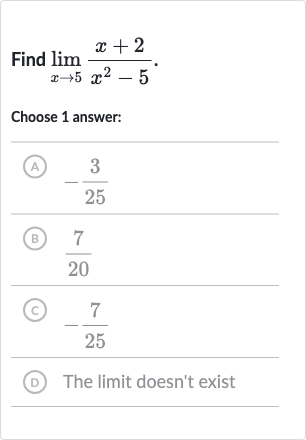
\newline

(C)

-\frac{7}{25}

\newline

(D) The limit doesn't exist

Substitute $x$ with $5$ : Substitute the value of $x$ with $5$ in the denominator to check if the limit can be directly calculated. $\newline$ $(5+2)/(5^2-5) = 7/(25-5) = 7/20$
Check if limit can be directly calculated: Since the denominator $5^2 - 5$ does not equal zero, we can directly substitute $x$ with $5$ in the numerator as well. $\newline$ The limit as $x$ approaches $5$ for the function $(x+2)/(x^2-5)$ is therefore $7/20$ .
Substitute $x$ with $5$ in numerator: Choose the correct option based on the calculation. $\newline$ The correct choice is (B) $\frac{7}{20}$ .