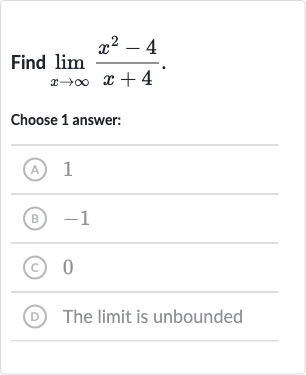
Find lim_(x rarr oo)(x^(2)-4)/(x+4). Choose 1 answer: (A) 1 (B) -1 (c) 0 (D) The limit is unbounded

Question

Find  lim_(x rarr oo)(x^(2)-4)/(x+4). Choose 1 answer: (A) 1 (B) -1 (c) 0 (D) The limit is unbounded

Bytelearn · Accepted Answer

Observing the highest power: To find the limit of the given function as x approaches infinity, we can use the properties of limits and the behavior of polynomials. lim_(x rarr oo)(x^(2)-4)/(x+4) We observe that the highest power of x in both the numerator and the denominator is x^2. To simplify, we can divide both the numerator and the denominator by x^2, the highest power of x present in the expression.Dividing numerator and denominator: Divide the numerator and the denominator by x^2: lim_(x rarr oo)((x^(2)/x^2) - (4/x^2))/(x/x^2 + 4/x^2) Simplify the expression: lim_(x rarr oo)(1 - 4/x^2)/(1/x + 4/x^2)Evaluating the limit of each term: As x approaches infinity, the terms with x in the denominator will approach zero. Therefore, we can evaluate the limit of each term individually: lim_(x rarr oo)(1) = 1 lim_(x rarr oo)(-4/x^2) = 0 lim_(x rarr oo)(1/x) = 0 lim_(x rarr oo)(4/x^2) = 0 Now we can rewrite the limit as: lim_(x rarr oo)(1 - 0)/(0 + 0)Simplifying the expression: The expression simplifies to: lim_(x rarr oo)(1)/(0) Since there are no terms with x in the denominator left, the limit simplifies to 1.

Find $\lim _{x \rightarrow \infty} \frac{x^{2}-4}{x+4}$ . $\newline$ Choose $1$ answer: $\newline$ (A) $1$ $\newline$ (B) $-1$ $\newline$ (C) $0$ $\newline$ (D) The limit is unbounded

Full solution

More problems from Add, subtract, multiply, and divide polynomials

Related topics

Find lim⁡x→∞x2−4x+4 \lim _{x \rightarrow \infty} \frac{x^{2}-4}{x+4} limx→∞​x+4x2−4​.\newlineChoose 111 answer:\newline(A) 111\newline(B) −1-1−1\newline(C) 000\newline(D) The limit is unbounded

Find $\lim _{x \rightarrow \infty} \frac{x^{2}-4}{x+4}$ . $\newline$ Choose $1$ answer: $\newline$ (A) $1$ $\newline$ (B) $-1$ $\newline$ (C) $0$ $\newline$ (D) The limit is unbounded