Full solution
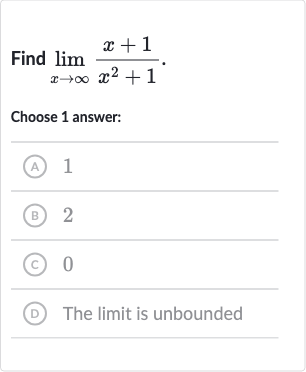
Q. Find .Choose answer:(A) (B) (C) (D) The limit is unbounded
- Analyze Behavior Separately: To find the limit of the function as approaches infinity, we need to analyze the behavior of the numerator and the denominator separately.
- Degree of Polynomials: The degree of the polynomial in the denominator is higher than the degree of the polynomial in the numerator . This means that as becomes very large, the denominator will grow much faster than the numerator.
- Simplify Expression: We can divide both the numerator and the denominator by , the highest power of in the denominator, to simplify the expression and see the behavior as approaches infinity.
- Approaching Infinity: As approaches infinity, the terms and in the numerator and the term in the denominator approach . So, the expression simplifies to .
- Limit Calculation: Therefore, the limit of as approaches is .