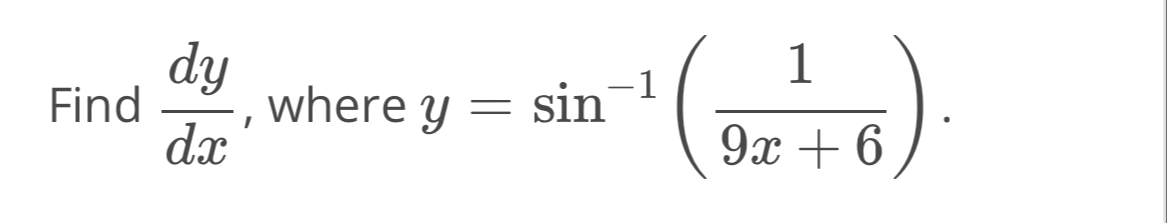Find (dy)/(dx), where y=sin^(-1)((1)/(9x+6))

Question

Find  (dy)/(dx), where  y=sin^(-1)((1)/(9x+6))

Bytelearn · Accepted Answer

Given function: We are given the function y = sin^(-1)((1)/(9x+6)). To find the derivative of y with respect to x, we will use the chain rule and the derivative of the inverse sine function.Derivative of inverse sine function: The derivative of the inverse sine function, sin^(-1)(u), with respect to u is 1/sqrt(1-u^2). Here, u = (1)/(9x+6). We will apply the chain rule to take the derivative of y with respect to x.Derivative of u with respect to x: First, we find the derivative of u with respect to x, where u = (1)/(9x+6). The derivative of 1/u with respect to u is -1/u^2, and the derivative of 9x+6 with respect to x is 9. So, the derivative of u with respect to x is -1/(9x+6)^2 * 9.Chain rule application: Now, we apply the chain rule: (dy)/(dx) = (dy)/(du) * (du)/(dx). We already have (dy)/(du) = 1/sqrt(1-u^2) and (du)/(dx) = -9/(9x+6)^2.Substitute u back: Substitute u back into the expression for (dy)/(du) to get (dy)/(du) = 1/sqrt(1-(1/(9x+6))^2).Multiply to find derivative: Now, multiply (dy)/(du) by (du)/(dx) to get the derivative of y with respect to x: (dy)/(dx) = (1/sqrt(1-(1/(9x+6))^2)) * (-9/(9x+6)^2).Simplify expression: Simplify the expression for (dy)/(dx) by combining the terms: (dy)/(dx) = -9/(9x+6)^2 * 1/sqrt(1-(1/(9x+6))^2).Further simplify expression: Further simplify the expression by combining the denominators: (dy)/(dx) = -9/((9x+6)^2 * sqrt(1-(1/(9x+6))^2)).

Find $\frac{d y}{d x}$ , where $y=\sin ^{-1}\left(\frac{1}{9 x+6}\right)$

Full solution

More problems from Evaluate expression when two complex numbers are given

Related topics

Find dydx \frac{d y}{d x} dxdy​, where y=sin⁡−1(19x+6) y=\sin ^{-1}\left(\frac{1}{9 x+6}\right) y=sin−1(9x+61​)

Find $\frac{d y}{d x}$ , where $y=\sin ^{-1}\left(\frac{1}{9 x+6}\right)$