Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find
(d)/(dx)(2cos 6x)
Answer:

Find $\frac{d}{d x}(2 \cos 6 x)$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Quotient property of logarithms

Full solution

Q. Find

\frac{d}{d x}(2 \cos 6 x)

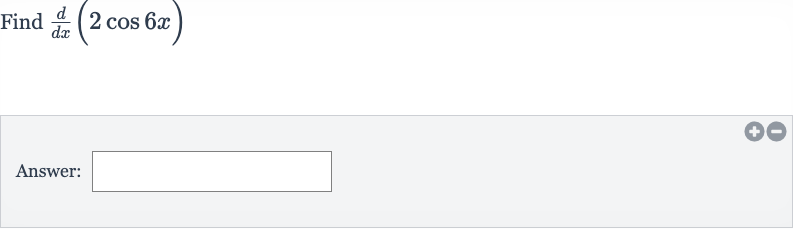
\newline

Answer:

Identify Function: Identify the function to differentiate. $\newline$ We need to find the derivative of the function $f(x) = 2\cos(6x)$ with respect to $x$ .
Apply Chain Rule: Apply the chain rule for differentiation. $\newline$ The chain rule states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function. $\newline$ Let's denote the outer function as $g(u) = 2\cos(u)$ and the inner function as $u(x) = 6x$ .
Differentiate Outer Function: Differentiate the outer function $g(u)$ with respect to $u$ . The derivative of $g(u) = 2\cos(u)$ with respect to $u$ is $g'(u) = -2\sin(u)$ , since the derivative of $\cos(u)$ is $-\sin(u)$ .
Differentiate Inner Function: Differentiate the inner function $u(x)$ with respect to $x$ . The derivative of $u(x) = 6x$ with respect to $x$ is $u'(x) = 6$ , since the derivative of $x$ with respect to $x$ is $1$ and we have a constant multiple of $6$ .
Apply Chain Rule Derivative: Apply the chain rule using the derivatives from steps $3$ and $4$ . $\newline$ The derivative of $f(x)$ with respect to $x$ is $f'(x) = g'(u) \cdot u'(x) = -2\sin(u) \cdot 6$ , where $u = 6x$ .
Substitute $u$ : Substitute $u = 6x$ back into the derivative. $\newline$ Substituting $u = 6x$ into the derivative, we get $f'(x) = -2\sin(6x) \times 6$ .
Simplify Derivative: Simplify the derivative. $\newline$ Simplifying the expression, we get $f'(x) = -12\sin(6x)$ .

More problems from Quotient property of logarithms

Question

Solve. Write your answer as an integer or a fraction in simplest form.

\newline

5^x=1

\newline

x=

Posted 3 months ago

Question

Steven opened a savings account and deposited

\$100.00

as principal. The account earns

9\%

interest, compounded annually. What is the balance after

5

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

\newline

\$

Posted 3 months ago

Question

Use the following function rule to find

f(1)

\newline

f(x) = 12(7)^x + 8

\newline

f(1) =

Posted 2 months ago

Question

The town of Valley View conducted a census this year, which showed that it has a population of

1,800

people. Based on the census data, it is estimated that the population of Valley View will grow by

12\%

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the town population,

y

x

decades after this census was taken.

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = 9^x

\newline

x =

Posted 3 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = e^x

\newline

x =

Posted 2 months ago

Question

Solve. Simplify your answer.

\newline

\log u = 1

\newline

u =

Posted 3 months ago

Question

Solve. Simplify your answer.

\newline

7\log x = 7

\newline

x =

Posted 2 months ago

Question

g(t) = 3^t

change over the interval from

t = 3

t = 4

\newline

\newline

g(t)

3

\newline

g(t)

3

\newline

g(t)

3\%

\newline

g(t)

200\%

Posted 3 months ago

Question

f(x)

6

over every unit interval in

x

f(0) = 0

\newline

Which could be a function rule for

f(x)

\newline

\newline

f(x) = 6^x

\newline

f(x) = 6x

\newline

f(x) = \frac{1}{6^x}

\newline

f(x) = \frac{x}{6}

Posted 3 months ago