AI tutor
Full solution
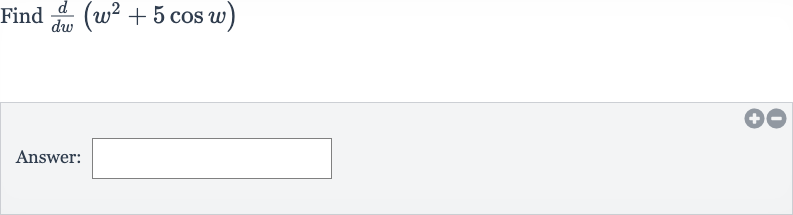
Q. Find Answer:
- Given function: We are given the function and we need to find its derivative with respect to , which is denoted as .
- Sum rule application: To find the derivative of the function, we will apply the sum rule of differentiation, which states that the derivative of a sum of functions is the sum of their derivatives. We will also use the power rule for the term and the chain rule for the term.
- Derivative of : First, let's find the derivative of the first term, . Using the power rule, which states that the derivative of is , we get:
- Derivative of : Now, let's find the derivative of the second term, . The derivative of with respect to is , and since we have a constant multiple of , we use the constant multiple rule to get:
- Combining derivatives: Combining the derivatives of both terms, we get the derivative of the entire function:
More problems from Evaluate expression when two complex numbers are given
QuestionGet tutor help
QuestionGet tutor help