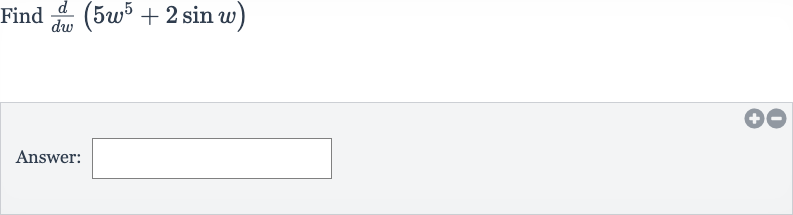
Find (d)/(dw)(5w^(5)+2sin w) Answer:

Question

Find  (d)/(dw)(5w^(5)+2sin w) Answer:

Bytelearn · Accepted Answer

Given Function: We are given the function f(w) = 5w^5 + 2sin(w), and we need to find its derivative with respect to w, which is denoted as (d/dw)(5w^5 + 2sin(w)).Sum Rule of Differentiation: To find the derivative of the function, we will apply the sum rule of differentiation, which states that the derivative of a sum of functions is the sum of their derivatives. We will differentiate each term separately.Differentiate 5w^5: First, we differentiate the term 5w^5 with respect to w. The power rule of differentiation states that if f(w) = w^n, then f'(w) = n*w^(n-1). Applying this rule, we get the derivative of 5w^5 as 5 * 5w^(5-1) = 25w^4.Differentiate 2sin(w): Next, we differentiate the term 2sin(w) with respect to w. The derivative of sin(w) with respect to w is cos(w). Therefore, the derivative of 2sin(w) is 2cos(w).Combine Derivatives: Now, we combine the derivatives of both terms to get the derivative of the entire function. The derivative of f(w) = 5w^5 + 2sin(w) with respect to w is 25w^4 + 2cos(w).Final Result: We have found the derivative without making any mathematical errors, and the final simplified form of the derivative is 25w^4 + 2cos(w).

Find $\frac{d}{d w}\left(5 w^{5}+2 \sin w\right)$ $\newline$ Answer:

Full solution

More problems from Evaluate expression when two complex numbers are given

Related topics

Find ddw(5w5+2sin⁡w) \frac{d}{d w}\left(5 w^{5}+2 \sin w\right) dwd​(5w5+2sinw)\newlineAnswer:

Find $\frac{d}{d w}\left(5 w^{5}+2 \sin w\right)$ $\newline$ Answer: