Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find all solutions of the equation below.

4^(3x+1)=7^(x)
The solution(s) is/are
x=
◻
(Simplify your answer. Use a comma to separate answers as needed. Round to four decimal places as needed.)

Find all solutions of the equation below. $\newline$ $4^{3 \mathrm{x}+1}=7^{x}$ $\newline$ The solution(s) is/are $x=$ $\square$ $\newline$ (Simplify your answer. Use a comma to separate answers as needed. Round to four decimal places as needed.)

View step-by-step help

View step-by-step help

Conjugate root theorems

Full solution

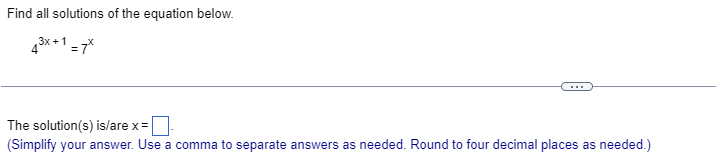
Q. Find all solutions of the equation below.

\newline

4^{3 \mathrm{x}+1}=7^{x}

\newline

The solution(s) is/are

x=

\square

\newline

(Simplify your answer. Use a comma to separate answers as needed. Round to four decimal places as needed.)

Take Logarithm: Take the logarithm of both sides to simplify the equation; using natural logarithm ( $\ln$ ) is common for such equations.
Apply Identity: Apply the logarithmic identity $\ln(a^b) = b\cdot\ln(a)$ to both sides.
Distribute $\ln(4)$ : Distribute $\ln(4)$ on the left side.
Rearrange Equation: Rearrange the equation to isolate terms involving $x$ on one side.
Factor Out $x$ : Factor out $x$ from the left side.
Solve for x: Solve for x by dividing both sides by $(3 \cdot \ln(4) - \ln(7))$ .
Calculate Value: Calculate the value using a calculator for precision, rounding to four decimal places as needed.

More problems from Conjugate root theorems

Question

Find the degree of this polynomial.

\newline

`5b^{10} + 3b^3`

\newline

Posted 2 months ago

Question

\newline

(9a + 5) - (2a + 4)

\newline

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

-3v^2(v^2 - 9)

\newline

Posted 1 month ago

Question

Find the product. Simplify your answer.

\newline

(v - 3)(4v + 1)

\newline

Posted 2 months ago

Question

Find the square. Simplify your answer.

\newline

(3y + 2)^2

\newline

Posted 2 months ago

Question

Divide. If there is a remainder, include it as a simplified fraction.

\newline

(24t^2 + 36t) \div 6t

\newline

Posted 2 months ago

Question

Is the function

q(x) = x^6 - 9

even, odd, or neither?

\newline

\newline

\text{[[even][odd][neither]]}

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

-3q^2(-3q^2 + q)

\newline

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

(r + 3)(4r + 2)

\newline

Posted 2 months ago

Question

Find the roots of the factored polynomial.

\newline

(x + 7)(x + 4)

\newline

Write your answer as a list of values separated by commas.

\newline

x =

Posted 2 months ago