Find all angles, 0^(@)

Question

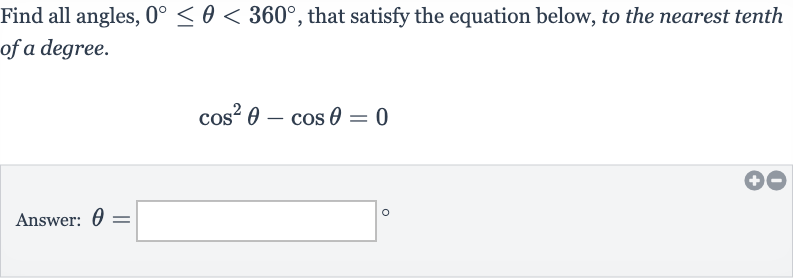
Find all angles,  0^(@) <= theta < 360^(@), that satisfy the equation below, to the nearest tenth of a degree.  cos^(2)theta-cos theta=0 Answer:  theta=

Bytelearn · Accepted Answer

Identify Trigonometric Equation: First, let's identify the trigonometric equation we need to solve: cos^2(theta) - cos(theta) = 0. We can factor this equation to find the values of theta that satisfy it. Factor out cos(theta): cos(theta)(cos(theta) - 1) = 0. Now we have two factors that can be individually set to zero to find the solutions for theta.Factor and Solve: Set the first factor equal to zero: cos(theta) = 0. To find the angles where the cosine of theta is zero, we look at the unit circle. Cosine is zero at 90 degrees (pi/2 radians) and 270 degrees (3pi/2 radians).Find Cosine Values: Set the second factor equal to zero: cos(theta) - 1 = 0. Solve for cos(theta): cos(theta) = 1. The angle where the cosine of theta is one is at 0 degrees (0 radians).Solve for Theta: Now we have all the angles that satisfy the equation within the range of 0 to 360 degrees. The angles are 0 degrees, 90 degrees, and 270 degrees. Convert these angles to the nearest tenth of a degree, which in this case does not change the values since they are already whole numbers.

Find all angles, 0^{\circ} \leq \theta<360^{\circ} , that satisfy the equation below, to the nearest tenth of a degree. $\newline$ $\cos ^{2} \theta-\cos \theta=0$ $\newline$ Answer: $\theta=$

Full solution

More problems from Find the roots of factored polynomials

Related topics

Find all angles, 0^{\circ} \leq \theta<360^{\circ} , that satisfy the equation below, to the nearest tenth of a degree.\newlinecos⁡2θ−cos⁡θ=0 \cos ^{2} \theta-\cos \theta=0 cos2θ−cosθ=0\newlineAnswer: θ= \theta= θ=

Find all angles, 0^{\circ} \leq \theta<360^{\circ} , that satisfy the equation below, to the nearest tenth of a degree. $\newline$ $\cos ^{2} \theta-\cos \theta=0$ $\newline$ Answer: $\theta=$