Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find all angles,
0^(@) <= theta < 360^(@), that satisfy the equation below, to the nearest tenth of a degree.

-2cos^(2)theta-3cos theta=1
Answer:
theta=

Find all angles, $0^{\circ} \leq \theta<360^{\circ}$ , that satisfy the equation below, to the nearest tenth of a degree. $\newline$ $-2 \cos ^{2} \theta-3 \cos \theta=1$ $\newline$ Answer: $\theta=$

View step-by-step help

View step-by-step help

Find the roots of factored polynomials

Full solution

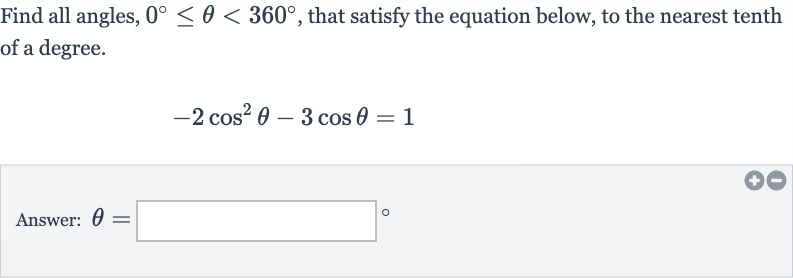
Q. Find all angles,

0^{\circ} \leq \theta<360^{\circ}

, that satisfy the equation below, to the nearest tenth of a degree.

\newline

-2 \cos ^{2} \theta-3 \cos \theta=1

\newline

Answer:

\theta=

Rewrite Equation with Variable: Let's first rewrite the equation in a more standard quadratic form by substituting $\cos(\theta)$ with a variable, let's say ' $x$ '. So, we have $-2x^2 - 3x = 1$ .
Set Equation to Zero: To solve for 'x', we need to set the equation to zero. So, we add $1$ to both sides of the equation to get $-2x^2 - 3x + 1 = 0$ .
Solve Quadratic Equation: Now, we need to solve the quadratic equation $-2x^2 - 3x + 1 = 0$ . We can use the quadratic formula, $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$ , where $a = -2$ , $b = -3$ , and $c = 1$ .
Calculate Discriminant: First, we calculate the discriminant, which is $b^2 - 4ac$ . Plugging in the values, we get $(-3)^2 - 4(-2)(1) = 9 + 8 = 17$ .
Find First Solution: Now, we can find the two solutions for 'x' using the quadratic formula. The first solution is $x = \frac{-(-3) + \sqrt{17}}{2 \cdot -2} = \frac{3 + \sqrt{17}}{-4}$ .
Find Second Solution: The second solution for 'x' is $x = \frac{-(-3) - \sqrt{17}}{2 \cdot -2} = \frac{3 - \sqrt{17}}{-4}$ .
Check Validity of Solutions: We need to check if these solutions for 'x' are within the range of the cosine function, which is between $-1$ and $1$ . Let's calculate the numerical values: $x_1 = (3 + \sqrt{17}) / -4$ and $x_2 = (3 - \sqrt{17}) / -4$ .
Calculate Angle for $x_2$ : Calculating the values, we get $x_1 \approx -1.28$ (which is not possible since the range of cosine is between $-1$ and $1$ ) and $x_2 \approx 0.28$ .
Find Second Angle: Since $x_1$ is not within the range of cosine, we discard it. Now, we need to find the angles $\theta$ for which $\cos(\theta) = x_2 \approx 0.28$ . We will use the inverse cosine function to find these angles.
Final Angles: Using a calculator, we find that $\cos^{-1}(0.28)$ gives us the principal value of $\theta$ , which is approximately $73.7$ degrees.
Final Angles: Using a calculator, we find that $\cos^{-1}(0.28)$ gives us the principal value of $\theta$ , which is approximately $73.7$ degrees.However, since the cosine function is positive in both the first and fourth quadrants, we need to find the second angle by subtracting the principal value from $360$ degrees. So, $360 - 73.7 = 286.3$ degrees.
Final Angles: Using a calculator, we find that $\cos^{-1}(0.28)$ gives us the principal value of $\theta$ , which is approximately $73.7$ degrees. However, since the cosine function is positive in both the first and fourth quadrants, we need to find the second angle by subtracting the principal value from $360$ degrees. So, $360 - 73.7 = 286.3$ degrees. We now have two angles that satisfy the original equation: $\theta \approx 73.7$ degrees and $\theta \approx 286.3$ degrees. These are the angles between $0$ and $360$ degrees that satisfy the equation $-2\cos^2(\theta) - 3\cos(\theta) = 1$ .

More problems from Find the roots of factored polynomials

Question

Find the degree of this polynomial.

\newline

`5b^{10} + 3b^3`

\newline

Posted 2 months ago

Question

\newline

(9a + 5) - (2a + 4)

\newline

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

-3v^2(v^2 - 9)

\newline

Posted 1 month ago

Question

Find the product. Simplify your answer.

\newline

(v - 3)(4v + 1)

\newline

Posted 2 months ago

Question

Find the square. Simplify your answer.

\newline

(3y + 2)^2

\newline

Posted 2 months ago

Question

Divide. If there is a remainder, include it as a simplified fraction.

\newline

(24t^2 + 36t) \div 6t

\newline

Posted 2 months ago

Question

Is the function

q(x) = x^6 - 9

even, odd, or neither?

\newline

\newline

\text{[[even][odd][neither]]}

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

-3q^2(-3q^2 + q)

\newline

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

(r + 3)(4r + 2)

\newline

Posted 2 months ago

Question

Find the roots of the factored polynomial.

\newline

(x + 7)(x + 4)

\newline

Write your answer as a list of values separated by commas.

\newline

x =

Posted 2 months ago