Find all angles, 0^(@)

Question

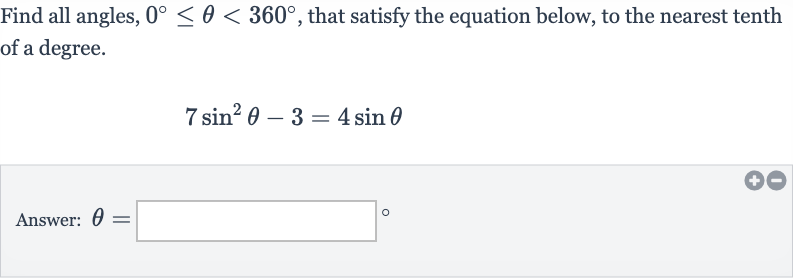
Find all angles,  0^(@) <= theta < 360^(@), that satisfy the equation below, to the nearest tenth of a degree.  7sin^(2)theta-3=4sin theta Answer:  theta=

Bytelearn · Accepted Answer

Rewrite Equation: Rewrite the given equation in a standard quadratic form. We have the equation 7sin^2(theta) - 3 = 4sin(theta). To solve for theta, we need to rearrange the equation into a standard quadratic form, ax^2 + bx + c = 0, where x is sin(theta). 7sin^2(theta) - 4sin(theta) - 3 = 0Factor Quadratic: Factor the quadratic equation. We need to factor the quadratic equation 7sin^2(theta) - 4sin(theta) - 3 = 0. This can be done by looking for two numbers that multiply to give -21 (7 * -3) and add to give -4. These numbers are -7 and 3. (7sin(theta) + 3)(sin(theta) - 1) = 0Solve Factors: Solve each factor for sin(theta). We now have two factors that can be set to zero to solve for sin(theta): 7sin(theta) + 3 = 0 or sin(theta) - 1 = 0 Solving each equation for sin(theta) gives us: sin(theta) = -3/7 or sin(theta) = 1Find sin(theta) = -3/7: Find the angles that correspond to sin(theta) = -3/7. Since sin(theta) = -3/7 does not correspond to a special angle, we will use a calculator to find the value of theta. We need to find the reference angle first and then determine the angles in the third and fourth quadrants where sine is negative. Reference angle = arcsin(3/7) ≈ 25.4 degrees Angles in the third and fourth quadrants: 180 + 25.4 = 205.4 degrees and 360 - 25.4 = 334.6 degreesFind sin(theta) = 1: Find the angles that correspond to sin(theta) = 1. The angle where sin(theta) = 1 is a special angle, and we know that sine reaches its maximum value of 1 at theta = 90 degrees.Compile Solutions: Compile all solutions. The angles that satisfy the original equation are approximately 205.4 degrees, 334.6 degrees, and 90 degrees.

Find all angles, 0^{\circ} \leq \theta<360^{\circ} , that satisfy the equation below, to the nearest tenth of a degree. $\newline$ $7 \sin ^{2} \theta-3=4 \sin \theta$ $\newline$ Answer: $\theta=$

Full solution

More problems from Find the roots of factored polynomials

Related topics

Find all angles, 0^{\circ} \leq \theta<360^{\circ} , that satisfy the equation below, to the nearest tenth of a degree.\newline7sin⁡2θ−3=4sin⁡θ 7 \sin ^{2} \theta-3=4 \sin \theta 7sin2θ−3=4sinθ\newlineAnswer: θ= \theta= θ=

Find all angles, 0^{\circ} \leq \theta<360^{\circ} , that satisfy the equation below, to the nearest tenth of a degree. $\newline$ $7 \sin ^{2} \theta-3=4 \sin \theta$ $\newline$ Answer: $\theta=$