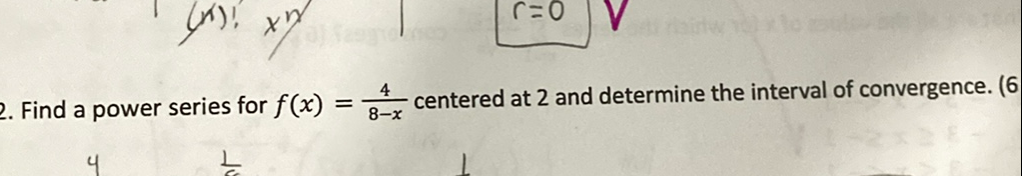AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Find a power series for centered at and determine the interval of convergence. (
Full solution
Q. Find a power series for centered at and determine the interval of convergence. (
- Rewrite Function: To find a power series for centered at , we first rewrite the function in a form that allows us to use the geometric series formula. The geometric series formula is , which converges when |r| < 1. We need to express in a similar form.
- Express as Geometric Series: We rewrite as . This puts the function in a form where we can identify the 'r' term for the geometric series as .
- Expand into Power Series: Now we can express as a geometric series: .
- Simplify Power Series: Using the geometric series formula, we expand into a power series: .
- Final Power Series: To simplify the power series, we distribute the across the series:
- Interval of Convergence: The power series for is now expressed as: .
- Check Endpoints: Next, we need to determine the interval of convergence for the power series. The series converges when |\frac{x-2}{6}| < 1, which means -1 < \frac{x-2}{6} < 1.
- Check Endpoints: Next, we need to determine the interval of convergence for the power series. The series converges when |\frac{x-2}{6}| < 1, which means -1 < \frac{x-2}{6} < 1.Solving the inequality for gives us -6 < x-2 < 6, which simplifies to -4 < x < 8.
- Check Endpoints: Next, we need to determine the interval of convergence for the power series. The series converges when |\frac{x-2}{6}| < 1, which means -1 < \frac{x-2}{6} < 1.Solving the inequality for gives us -6 < x-2 < 6, which simplifies to -4 < x < 8.We must check the endpoints and to see if the series converges at these points. For , the series becomes , which is a finite number. For , the series is undefined because it would involve division by zero. Therefore, the interval of convergence is -1 < \frac{x-2}{6} < 1.
