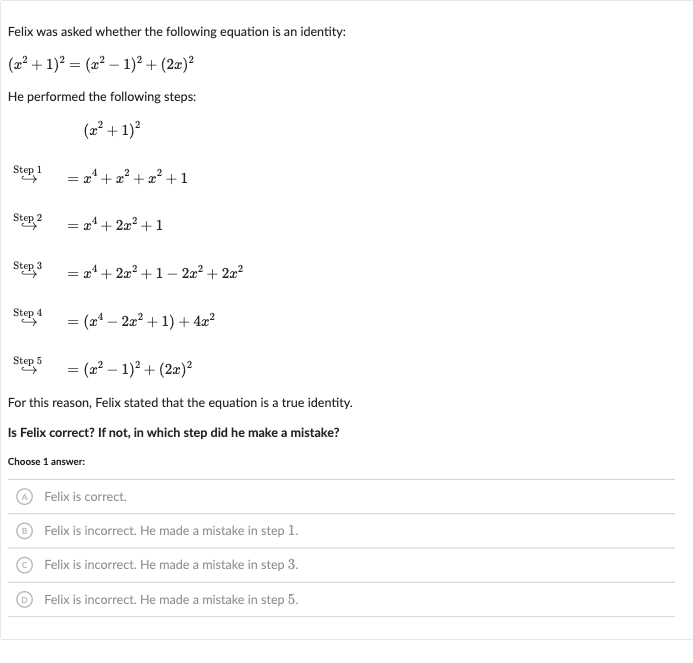
Felix was asked whether the following equation is an identity: $\newline$ $\left(x^{2}+1\right)^{2}=\left(x^{2}-1\right)^{2}+(2 x)^{2}$ $\newline$ He performed the following steps: $\newline$ $\left(x^{2}+1\right)^{2}$ $\newline$ $\stackrel{\text { Step } 1}{\hookrightarrow}=x^{4}+x^{2}+x^{2}+1$ $\newline$ $\stackrel{\text { Step } 2}{\hookrightarrow}=x^{4}+2 x^{2}+1$ $\newline$ $\stackrel{\text { Step } 3}{\hookrightarrow}=x^{4}+2 x^{2}+1-2 x^{2}+2 x^{2}$ $\newline$ $\stackrel{\text { Step } 4}{\hookrightarrow}=\left(x^{4}-2 x^{2}+1\right)+4 x^{2}$ $\newline$ $\stackrel{\text { Step } 5}{\hookrightarrow}=\left(x^{2}-1\right)^{2}+(2 x)^{2}$ $\newline$ For this reason, Felix stated that the equation is a true identity. $\newline$ Is Felix correct? If not, in which step did he make a mistake? $\newline$ Choose $1$ answer: $\newline$ (A) Felix is correct. $\newline$ (B) Felix is incorrect. He made a mistake in step $1$ . $\newline$ (C) Felix is incorrect. He made a mistake in step $3$ . $\newline$ (D) Felix is incorrect. He made a mistake in step $5$ .

Full solution

Q. Felix was asked whether the following equation is an identity:

\newline

\left(x^{2}+1\right)^{2}=\left(x^{2}-1\right)^{2}+(2 x)^{2}

\newline

He performed the following steps:

\newline

\left(x^{2}+1\right)^{2}

\newline

\stackrel{\text { Step } 1}{\hookrightarrow}=x^{4}+x^{2}+x^{2}+1

\newline

\stackrel{\text { Step } 2}{\hookrightarrow}=x^{4}+2 x^{2}+1

\newline

\stackrel{\text { Step } 3}{\hookrightarrow}=x^{4}+2 x^{2}+1-2 x^{2}+2 x^{2}

\newline

\stackrel{\text { Step } 4}{\hookrightarrow}=\left(x^{4}-2 x^{2}+1\right)+4 x^{2}

\newline

\stackrel{\text { Step } 5}{\hookrightarrow}=\left(x^{2}-1\right)^{2}+(2 x)^{2}

\newline

For this reason, Felix stated that the equation is a true identity.

\newline

Is Felix correct? If not, in which step did he make a mistake?

\newline

Choose

1

answer:

\newline

(A) Felix is correct.

\newline

(B) Felix is incorrect. He made a mistake in step

1

\newline

3

\newline

(D) Felix is incorrect. He made a mistake in step

5

Expand Left Side: Expand the left side of the equation $(x^{2}+1)^{2}$ . $\newline$ Calculation: $(x^{2}+1)(x^{2}+1) = x^{4} + 2x^{2} + 1$
Expand Right Side: Expand the right side of the equation $(x^{2}-1)^{2}+(2x)^{2}$ . $\newline$ Calculation: $(x^{2}-1)(x^{2}-1) + (2x)(2x) = x^{4} - 2x^{2} + 1 + 4x^{2}$
Combine Like Terms: Combine like terms on the right side. $\newline$ Calculation: $x^{4} - 2x^{2} + 1 + 4x^{2} = x^{4} + 2x^{2} + 1$
Compare Expanded Forms: Compare the expanded forms of both sides. $\newline$ Calculation: Left side = $x^{4} + 2x^{2} + 1$ , Right side = $x^{4} + 2x^{2} + 1$
Determine Identity: Determine if the equation is an identity. $\newline$ Calculation: Since both sides are equal, the equation is an identity.