AI tutor
Full solution
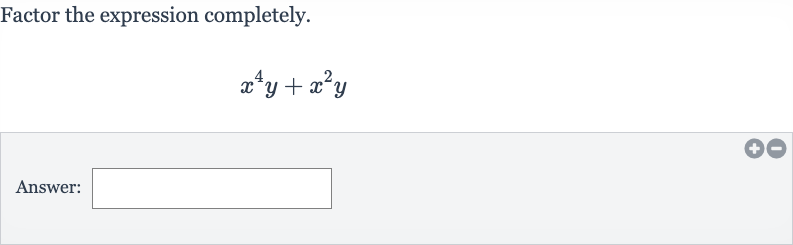
Q. Factor the expression completely.Answer:
- Identify Factors: Identify common factors in both terms.Both terms and have and as common factors.
- Factor Out GCF: Factor out the greatest common factor (GCF). The GCF of and is . So we factor out of both terms.
- Check Further Factoring: Check if the remaining expression inside the parentheses can be factored further.The expression inside the parentheses is , which cannot be factored further over the real numbers because it does not have real roots.
More problems from Composition of linear and quadratic functions: find an equation
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help